YOLOv8のモデルを作成した後は、モデルの精度を確認する必要があります。
これは人間の目でpredictによる出力結果を確認する方法が最も確からしいと思いますが、確認する人によって結果がブレる可能性があるのと様々なパターンを用意することにより確認する枚数が100枚や1000枚を超えてくるといくら時間があっても足りないですよね。
ちなみに私の場合ですが、ニューラルネットワークのウェイトの初期値がランダムである場合、学習の進捗具合が毎回異なるので少なくとも同じデータセットではモデルを3回以上を同じパラメータで作成することにしています。
※ YOLOv8のtrainの場合、seedが設定できるので同じシード値の場合は同じ結果になるのかも? 何回か作ってみて確認する必要あり
物体検知モデルの精度確認の指標には色々あります。何となく今まで昔の記事でまとめていた気になっていたのですが、「⑤ アンバランスデータの処理 (imbalaced data processing)」のセクションににて正解率と再現率にて少し言及した程度でした 笑
今回各指標の理解とまとめだけでかなりのボリュームになってしまったので、実画像で色々確認するのは次の記事にしようと思います。
物体検知の予測結果が正しいか間違っているかの判断について
タイタニック生存有無の判別であれば、たとえば予測確率が0.5以上は「1:生存」、0.5より下は「0:非生存」と定義し正解ラベルと比較することで精度を確認することが出来ます。
それが物体検知になり、写真のどこかに存在する猫を見つけたい場合だと予測確率(例:猫である確率)に加えて、予測した物体の位置関係も考慮しないと正しい精度を計算することは難しくなります。(MNISTデータセットのように数字が決められたサイズの画像の中心に常に存在する場合は気にしなくてもいいかも知れませんが)
「分類」と「物体検知」の違いについてはTowards Data Scienceさんの「What is Average Precision in Object Detection & Localization Algorithms and how to calculate it?」という記事が分かりやすいです。
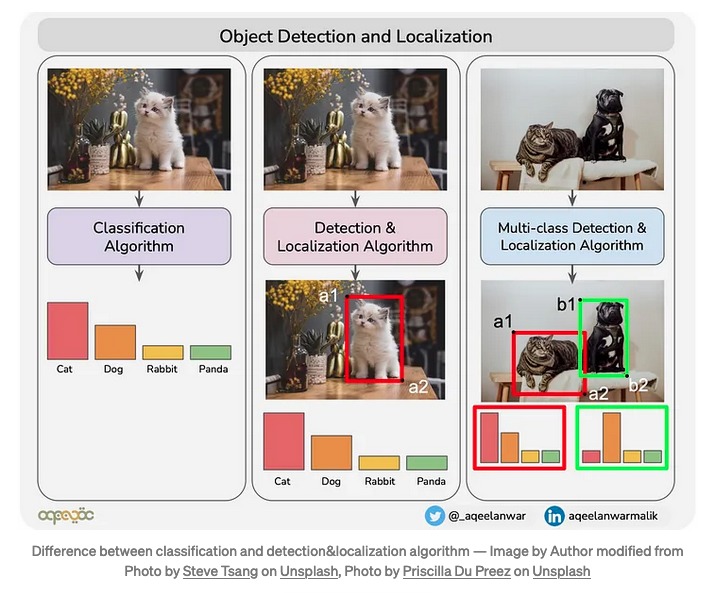
下記はYOLOv8のyolov8n.ptで物体検知した結果になりますが、確信度が0.39のバウンディングボックスは幅広すぎて正しく猫の位置を推定できていないことが分かります。確信度が0.34のバウンディングボックスは何となく黒い猫ちゃんを正しく検知出来ていそうですよね。

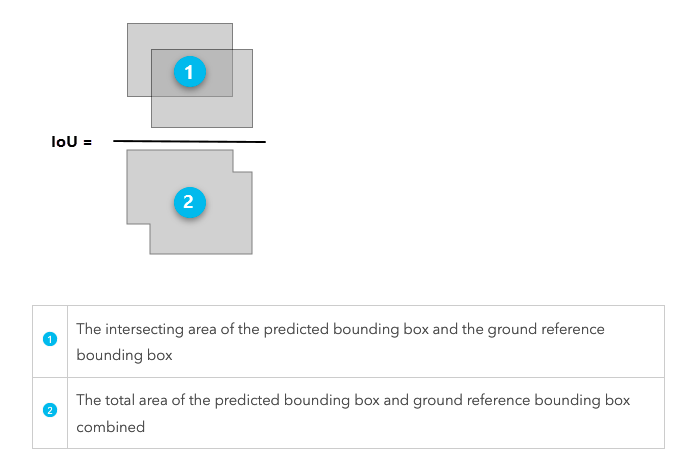
このような場合、モデルで「猫と予測した部分」と「実際にこの部分は猫である」という正解情報の2つの重なり具合(IoU ratio)を計算することで検知結果が正しいか判断し精度を確認することが可能になるようです。枚数が少なければ目視で合ってる合っていないをBBOX毎に判断しても良いと思います。(その方が楽ですね)
The Intersection over Union (IoU) ratio is used as a threshold for determining whether a predicted outcome is a true positive or a false positive.
引用: https://pro.arcgis.com/en/pro-app/latest/tool-reference/image-analyst/how-compute-accuracy-for-object-detection-works.htm
物体検知の評価指標まとめ
評価指標はおおよそタイタニックの生存者分析などの分類問題にも当てはめることができると思います。
単独の指標だけで判断するのではなく、複数の評価指標と併せて総合的にモデルの性能を評価することが良いようです。
個人的には、「Accuracy (正解率)」・「AP もしくは mAP」・「可能であれば誤検知率 (〇〇と認識したけど実際は違う)」らへんを確認して総合的にモデルの精度を判断するのがいいかなと思っています。
下記で基礎的な情報であるTP、TN、FP、FNの概念について「猫の検出」を例にまとめておきます。
分類問題の参考書だと病気の陽性・陰性で例えられることが多いかも知れません。
■ TP、TN、FP、FNのまとめ
・TPはTrue Positive(真陽性)であり、モデルが実際に猫検出し、それが正解であった数を示します。
・TNはTrue Negative(真陰性)であり、モデルが実際に背景を背景として検出し、それが正解であった数を示します。(つまり猫がいない画像は正しく何も検知しなかったという意味)
・FPはFalse Positive(偽陽性)であり、モデルが実際には背景であるにもかかわらず物体を誤って検出した数を示します。(つまり誤検知)
・FNはFalse Negative(偽陰性)であり、モデルが実際には猫であるにもかかわらず検出を見逃した数を示します。(つまり未検知)
100枚の猫画像への検知結果を例として考えてみた
ここからは、物体検知モデルで100枚の猫画像を評価し下記のような結果になったと仮定し評価指標を計算してみようと思います。
実際に猫が存在する画像は85枚、15枚は猫が写っていない画像と仮定します。(猫が存在する画像は1枚の画像につき1匹のみ猫が存在すると考えた方がしっくりくるかも知れません)
・70枚の猫が存在する画像で猫を正しく検出 (TP)
・5枚の猫が存在しない画像で猫を検出しない (TN)
・10枚の猫が存在しない画像で猫だと検出 (FP)
・15枚の猫が存在する画像で猫を検出できなかった場合 (FN)
1枚の画像に100匹の猫がいる方が分かりやすかったでしょうか。
TNの説明が分かりにくくなりますので単位を画像の枚数にしましたが、適時読み替えていただければと思います 笑
Accuracy (正解率)
「Accuracy(正解率)」は、モデルが正しく物体を検出し、かつ正しく背景を背景として検出できた割合を示します。
数式だと下記のようになります。
Accuracy = (TP + TN) / (TP + FP + TN + FN)
仮定を元に計算すると、正解率は90%という結果になります。
Accuracy = (TP + TN) / (TP + FP + TN + FN)
= (70 + 5) / (70 + 10 + 5 + 15)
= 75 / 100
= 0.75 (75%)
Precision (適合率)
「Precision (適合率)」は、モデルが物体として検出した中で、実際に物体であるものの割合を示します。
数式だと下記のようになります。
Precision = TP / (TP + FP)
仮定を元に計算すると、適合率は94.1%という結果になります。
Precision = TP / (TP + FP)
= 70 / (70 + 10)
= 0.875 (87.5%)
つまり、100枚のうち80枚で猫を検知したが、そのうち70枚が本当に猫の画像で10枚は誤検知だったという意味になります。
猫を検知するモデルの「正確性」は87.5%になるということですね。
Recall (再現率)
「Recall (再現率)」は、実際に物体であるものの中で、モデルが正しく物体を検出した割合を示します。
数式だと下記のようになります。
Recall = TP / (TP + FN)
仮定を元に計算すると、再現率は94.1%という結果になります。
Recall = TP / (TP + FN)
= 70 / (70 + 15)
= 0.8235 (82.4%)
つまり、実際に猫が存在する85枚の画像のうち、70枚を正しく検出できたことを示しています。
猫を検知するモデルの「網羅性」は82.4%になるということみたいです。
網羅性か正確性を選択するかはタスクによって考えないといけないですね。例えば病気の可能性を探るものとしては網羅性が高い方がいいかも知れませんし、顔認証みたいなセキュリティ関係は正確性を重視した方がいい場合が多そうです。
F1 Score
「F1スコア」は、適合率(Precision)と再現率(Recall)の調和平均を示す指標であり、適合率と再現率の両方を考慮してモデルの性能を評価します。
数式だと下記のようになります。
F1 Score = 2 * (Precision * Recall) / (Precision + Recall)
仮定を元に計算すると、F1スコアは0.85という結果になります。
F1 Score = 2 (Precision Recall) / (Precision + Recall)
= 2 (0.875 0.8235) / (0.875 + 0.8235)
= 0.85
つまり、適合率と再現率のバランスを考慮した性能評価指標であり、モデルが物体検知タスクをどれだけ正確に実行できているかを示しています。
F1スコアが高いほど、モデルが適合率と再現率の両方を高い水準で実現していることを示し、モデルの性能が優れていることを示します。
ただ現実問題では、適合率と再現率はトレードオフの関係にあり一方を高めると他方が低くなる傾向にあります。
計算しておくものの個人的にモデル採用時の基準としては分かりずらかったので私はそこまで活用したことはないです。
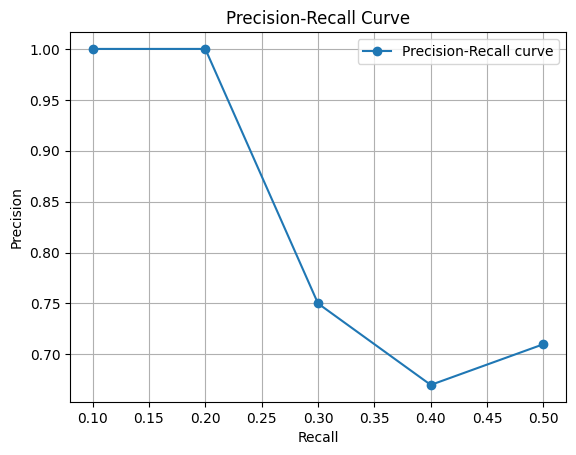
Precision-Recall Curve (PR曲線)
「Precision-Recall Curve(PR曲線)」は、モデルの検出結果を確率やIoUなど何かしらの閾値を変化させながら評価し適合率と再現率の関係を可視化したものです。
F1スコアでも記載しましたが、適合率と再現率はトレードオフの関係にあります。適合率を上げると、誤検出が減りますが検出漏れが増える可能性があります。一方、再現率を上げると、検出漏れが減りますが誤検出が増える可能性があります。適合率と再現率のバランスを見つけることが重要です。
今回は例として物体検知モデルで検知する際の「確信度」の閾値を変更し、それぞれの検知結果の適合率と再現率を計算したと仮定してPR曲線を描画してみます。下記引用先を参考にしました。
A precision-recall curve plots the value of precision against recall for different confidence threshold values.
引用: https://towardsdatascience.com/what-is-average-precision-in-object-detection-localization-algorithms-and-how-to-calculate-it-3f330efe697b
サンプルですが、物体検出時の確信度の閾値を変更したときの検知結果の表を作成しました。(私の創作です)
確信度の閾値を高く設定することで誤検出(FP)を減らし適合率を向上させることができます。
ただし確率が低い物体は検出されなくなるので、未検知(FN)が増える可能性があります。
逆に閾値を低くするとモデルがより多くの検出結果を出力するようになり未検知(FN)が減り再現率が向上します。
ただし確率が低い物体も検出するようになるので誤検知(FP)が増える可能性があります。
このようにPR曲線を確認することによって、どの閾値が取り組んでいるタスクで許容できる結果になるのか探れそうですね。
| conf閾値 | TP | FP | FN | Precision (TP / (TP + FP)) | Recall (TP / (TP + FN)) |
|---|---|---|---|---|---|
| 0.1 | 85 | 25 | 0 | 85 / (85 + 25) = 0.772 | 85 / (85 + 0) = 1.000 |
| 0.2 | 85 | 20 | 0 | 85 / (85 + 20) = 0.809 | 85 / (85 + 0) = 1.000 |
| 0.3 | 85 | 15 | 0 | 85 / (85 + 15) = 0.850 | 85 / (85 + 0) = 1.000 |
| 0.4 | 85 | 12 | 0 | 85 / (85 + 12) = 0.876 | 85 / (85 + 0) = 1.000 |
| 0.5 | 70 | 10 | 15 | 70 / (70 + 10) = 0.875 | 70 / (70 + 15) = 0.824 |
| 0.6 | 60 | 8 | 25 | 60 / (60 + 8) = 0.882 | 60 / (60 + 25) = 0.706 |
| 0.7 | 50 | 5 | 35 | 50 / (50 + 5) = 0.909 | 50 / (50 + 35) = 0.588 |
| 0.8 | 40 | 3 | 45 | 40 / (40 + 3) = 0.930 | 40 / (40 + 45) = 0.471 |
| 0.9 | 30 | 2 | 55 | 30 / (30 + 2) = 0.938 | 30 / (30 + 55) = 0.353 |
| 1.0 | 25 | 1 | 60 | 25 / (25 + 1) = 0.962 | 25 / (25 + 60) = 0.294 |
※ TNは適合率と再現率の計算に使われないので記載していません。
import matplotlib.pyplot as plt
# PrecisionとRecallの値をリストに格納
thresholds = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
precision = [0.772, 0.809, 0.850, 0.876, 0.875, 0.882, 0.909, 0.930, 0.938, 0.962]
recall = [1.000, 1.000, 1.000, 1.000, 0.824, 0.706, 0.588, 0.471, 0.353, 0.294]
# PR曲線を描画
plt.plot(recall, precision, marker='o')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall Curve')
plt.grid(True)
plt.show()
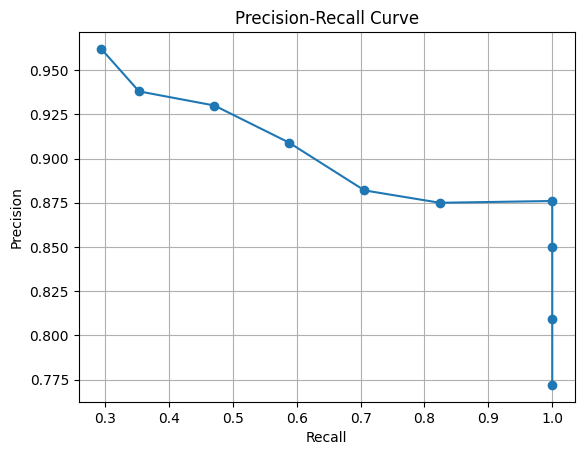
私だったら、全ての猫を補足できて誤検知もまぁまぁ許容できるconf=0.4 (適合率は0.876、再現率は1.000)を選択すると思います。
物体検知でよく使われる精度指標であるAverage Precision(AP)を計算するためのPR曲線
上記のセクションでは最適な閾値を求めるためにPR曲線を求めました。
例えば2値分類タスクの機械学習で予測スコアを付与した後に、1と0の境目のスコアを最適化する時などに活用できると思います。(0.5を閾値にするより0.4にするなどが考えられます)
しかし色々調べていて、物体検知の精度指標であるAPはPR曲線下の面積の値をモデル評価値としているようで適合率と再現率の計算方法は下記のように累積TPと累積FPが使われている様です。(複数クラスが存在する場合は1クラスずつ確認する)
○ 計算式:
・適合率 = 累積TP / ( 累積 TP + 累積FP )
・再現率 = 累積TP / 確認中のクラスに属する物体の総数
悩んだのですが、前セクションの閾値の変化による適合率と再現率の計算と区別するために「Average Precision(AP)を計算するためのPR曲線」とカテゴライズすることにしました。
APの概要はWikipediaに記載されており、ランク付けされたシーケンスに対して各順位ごとに適合率と再現率を計算することによって算出できるようです。
情報検索(information retrival)のカテゴリにあったので、検索アルゴリズムの精度確認とかでも使えそうですかね。
By computing a precision and recall at every position in the ranked sequence of documents, one can plot a precision-recall curve
引用: https://en.wikipedia.org/wiki/Evaluation_measures_(information_retrieval)#Average_precision
APの詳細は犬の画像を例に「Mean Average Precision (mAP) in Object Detection」で詳しくまとめてくださっていますので、参考にさせていただきました。
○ PR曲線作成手順:
APを計算するまでの流れとしては下記のようになっているようです。
- モデルで検知した物体をスコアの高い順に並べる
- IoUや目視で正確に検知できているのか(TP)、それとも誤検知(FP)なのかを判断する
- 累積TPと累積FPを計算し、適合率と再現率を計算
- PR曲線を描く
- 様々なやり方でPR曲線下の面積(AUC)を計算し、APを算出する (11point interpolation method、PR-AUC、101point interpolation methodなどの手法があるようです)
○ 作成例:
下記は10匹の猫がいる画像に対して物体検知をした結果例の表になります。(こちらも私の創作になります)
「1匹は検知できず」、その他9匹は「5匹正しく検出」、「4匹は間違って検出」されたとします。(正誤判定に関しては目視で確認したか、IoUは0.5と仮定しています。)
| 検知した物体# | 確信度 | 正誤判定(TP or FP) | 累積TP | 累積FP | 適合率(Precision) | 再現率(Recall) |
|---|---|---|---|---|---|---|
| #3 | 0.92 | TP | 1 | 0 | 1/(1+0)=1.00 | 1/10=0.1 |
| #5 | 0.91 | FP | 2 | 0 | 2/(2+0)=1.00 | 2/10=0.2 |
| #2 | 0.88 | TP | 2 | 1 | 2/(2+1)=0.67 | 2/10=0.2 |
| #1 | 0.86 | FP | 3 | 1 | 3/(3+1)=0.75 | 3/10=0.3 |
| #6 | 0.77 | TP | 3 | 2 | 3/(3+2)=0.60 | 3/10=0.3 |
| #9 | 0.63 | TP | 4 | 2 | 4/(4+2)=0.67 | 4/10=0.4 |
| #8 | 0.58 | TP | 5 | 2 | 5/(5+2)=0.71 | 5/10=0.5 |
| #7 | 0.21 | FP | 5 | 3 | 5/(5+3)=0.63 | 5/10=0.5 |
| #6 | 0.15 | FP | 5 | 4 | 5/(5+4)=0.56 | 5/10=0.5 |
import matplotlib.pyplot as plt
# データの準備
precision = [1.0, 1.0, 0.67, 0.75, 0.60, 0.67, 0.71, 0.63, 0.56]
recall = [0.1, 0.2, 0.2, 0.3, 0.3, 0.4, 0.5, 0.5, 0.5]
# Precision-Recall curveを描画
plt.plot(recall, precision, marker='o', label='Precision-Recall curve')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall curve')
plt.legend(loc='lower left')
plt.grid(True)
plt.show()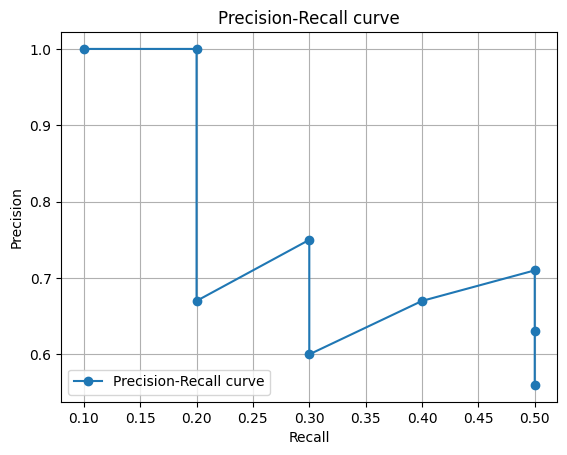
よく物体検知の論文などで見かけるジグザグのラインになりましたね 笑
ただ、もし複数の適合率(Precision)の値が同じ再現率(Recall)の値を持つ場合は、APの値には影響ないので簡略化のために一番適合率が高い行のみを残せばいいようです。
Note: If the table contains multiple precision values for the same recall values, you can consider the highest value and discard the rest. Not doing so will NOT affect the final result.
引用: https://learnopencv.com/mean-average-precision-map-object-detection-model-evaluation-metric/
簡略した場合、下記の様な感じになりますでしょうか。
| 検知した物体# | 確信度 | 正誤判定(TP or FP) | 累積TP | 累積FP | 適合率(Precision) | 再現率(Recall) |
|---|---|---|---|---|---|---|
| #3 | 0.92 | TP | 1 | 0 | 1/(1+0)=1.00 | 1/10=0.1 |
| #5 | 0.91 | FP | 2 | 0 | 2/(2+0)=1.00 | 2/10=0.2 |
| #1 | 0.86 | FP | 3 | 1 | 3/(3+1)=0.75 | 3/10=0.3 |
| #9 | 0.63 | TP | 4 | 2 | 4/(4+2)=0.67 | 4/10=0.4 |
| #8 | 0.58 | TP | 5 | 2 | 5/(5+2)=0.71 | 5/10=0.5 |
実際に次のセクションでAPを計算するので結果が変わらないか確認してみようと思います。
Average Precision (AP:平均適合率)
Average Precision(AP:平均適合率)は「PR曲線下の面積」を計算したもので、0から1の値を取ります。通常1クラスずつ算出した結果を指しますが、複数のクラスのAPを算出し平均値を取ったmAPのことをAPと呼ぶ場合もあるようです。(参考: detection evaluation metrics used by COCO)。APが1だと適合率と再現率が全て1だという意味になり、画像内に存在する個別クラスのオブジェクトを全て1つの間違いもなく検知できたという意味になります。※ 正確にはground truthデータと呼ばれる正解データと予測したデータがIoU=0.5などで全一致したということになるかと思います。
実は調べてみるとAPの計算方法はいくつか方法があるようです。
PR曲線のセクションで参考にした「Mean Average Precision (mAP) in Object Detection」やBrno University of Technologyのレクチャーノート「mAP for Object Detection」にてPASCAL VOCやMS COCOといった有名な物体検知用のデータセットでベンチマークとして使っているAPの計算方法についてまとめられています。
とりあえずメジャーな計算方法として、11点補完AP、PR-AUC、101点補完APの3つを覚えておけば良さそうです。ちなみに23年4月現在COCOデータセットで使われる「101点補完AP」がスタンダードな手法なようです。
11 Point Interpolation Method ... was introduced in the 2007 PASCAL VOC challenge. It is calculated at IoU threshold 0.5.
PR-AUC is the exact area under the Precision-Recall curve [used in PASCAL VOC 2010]
MS COCO introduced 101 Point Interpolation AP in 2014...At present, MS COCO 101 point Average Precision (AP) is accepted as the standard metric.
引用: https://learnopencv.com/mean-average-precision-map-object-detection-model-evaluation-metric/
それぞれのAPの計算方法の詳細を公式ページやソースコードから見つけましたので、まとめておきます。
11 Point Interpolation AP (11点補完AP)
PASCAL VOC challenge 2007 ~ 2009まで使われていた計算方法になります。
Example code for computing the precision/recall and AP measure is provided in the development kit.
Note that this differs from the VOC2006 evaluation measure.
引用: http://host.robots.ox.ac.uk/pascal/VOC/voc2007/devkit_doc_07-Jun-2007.pdf
voc2007のページからダウンロードできるdevelopment kitのソースコードを確認すると、VOCdevkit -> VOCcode -> VOCevaldet.m内に11 point interpolated APを計算していそうな記述がありました。
% compute precision/recall
fp=cumsum(fp);
tp=cumsum(tp);
rec=tp/npos;
prec=tp./(fp+tp);
% compute average precision
ap=0;
for t=0:0.1:1
p=max(prec(rec>=t));
if isempty(p)
p=0;
end
ap=ap+p/11;
end
引用: VOCevaldet.m
PR-AUC (All points APと紹介しているところもありました)
PASCAL VOC challenge 2010から使われる様になった計算方法です。「How to calculate mAP for detection task for the PASCAL VOC Challenge?」らへんもサンプルデータがあったので勉強になりました。
The computation of the average precision (AP) measure was changed in 2010
to improve precision and ability to measure differences between methods with
low AP. It is computed as follows:
- Compute a version of the measured precision/recall curve with precision
monotonically decreasing, by setting the precision for recall r to the max-
imum precision obtained for any recall r′ ≥ r.- Compute the AP as the area under this curve by numerical integration.
No approximation is involved since the curve is piecewise constant.
Note that prior to 2010 the AP is computed by sampling the monotonically
decreasing curve at a fixed set of uniformly-spaced recall values 0, 0.1, 0.2, . . . , 1.
By contrast, VOC2010–2012 effectively samples the curve at all unique recall
values.
引用: http://host.robots.ox.ac.uk/pascal/VOC/voc2012/devkit_doc.pdf [3.4.1 Average Precision (AP)]
101 Point Interpolation AP (101点補完AP)
MS COCOが101 Point Interpolation APを精度検証の指標に使っているというエビデンスが中々見つかりませんでしたが、cocoapiのgithubのチケット「 Question about AP definition #268 」にソース上に記載があるとやり取りがありましたので該当部分を見つけました。
cocoapi/PythonAPI/pycocotools/cocoeval.py
Line 26 in 636becd
recThrs - [0:.01:1] R=101 recall thresholds for evaluationcocoapi/PythonAPI/pycocotools/cocoeval.py
Line 507 in 636becd
self.recThrs = np.linspace(.0, 1.00, np.round((1.00 - .0) / .01) + 1, endpoint=True)
引用: cocoeval.py
11点補完APの計算と描画
# 補完Precisionのラインを描画するためだけのリスト作成
def create_pr_auc_list(recall_interpolated,precision_interpolated):
_precision_interp_line = []
_recall_interp_line = []
previous_precision=None
previous_recall=None
for curr_recall, curr_precision in zip(recall_interpolated, precision_interpolated):
# 先頭行 or 同じprecisionの場合
if curr_precision == previous_precision or previous_precision is None:
_precision_interp_line.append(curr_precision)
_recall_interp_line.append(curr_recall)
# precisionが異なる場合
else:
# 描画用のプロットを追加
_precision_interp_line.append(curr_precision)
_recall_interp_line.append(previous_recall)
_precision_interp_line.append(curr_precision)
_recall_interp_line.append(curr_recall)
# 情報の保持
previous_precision = curr_precision
previous_recall = curr_recall
return (_recall_interp_line,_precision_interp_line)
# 補完AP計算と描画 (interp_pointsは11 or 101)
def draw_interp_pr_auc(precision,recall,interp_points):
import matplotlib.pyplot as plt
import numpy as np
# num-Point Interpolation AP calculation
num_interpolated_points = interp_points
recall_interp = np.linspace(0, 1, num_interpolated_points)
precision_interp = np.zeros(num_interpolated_points)
for i in range(num_interpolated_points):
for j in range(len(recall)):
if recall[j] >= recall_interp[i]:
precision_interp[i] = max(precision_interp[i], precision[j])
ap = np.sum(precision_interp) / num_interpolated_points
precision_interp_line = []
recall_interp_line = []
# PR-AUCの描画用
recall_interp_line,precision_interp_line = create_pr_auc_list(recall_interp,precision_interp)
# Precision-Recall curveを描画
plt.plot(recall, precision, marker='o', markersize=5, label='Precision-Recall curve')
plt.scatter(recall_interp, precision_interp, color="#ff7f0e", marker='s',s=80,label="Interpolated Points")
plt.plot(recall_interp_line, precision_interp_line,linestyle='dotted', color="#ff7f0e", linewidth=2)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall curve with Interpolated Points')
plt.legend()
plt.grid(True)
plt.show()
print(str(interp_points) + ' Point Interpolation Average Precision (AP): {:.4f}'.format(ap))
return apPR曲線のセクションで作成した下記サンプルデータで試してみます。
下記は10匹の猫がいる画像に対して物体検知をした結果例の表になります。(こちらも私の創作になります)
「1匹は検知できず」、その他9匹は「5匹正しく検出」、「4匹は間違って検出」されたとします。(正誤判定に関しては目視で確認したか、IoUは0.5と仮定しています。)
precision = [1.0, 1.0, 0.67, 0.75, 0.60, 0.67, 0.71, 0.63, 0.56]
recall = [0.1, 0.2, 0.2, 0.3, 0.3, 0.4, 0.5, 0.5, 0.5]
ap = draw_interp_pr_auc(precision,recall,11)11 Point Interpolation Average Precision (AP): 0.4664
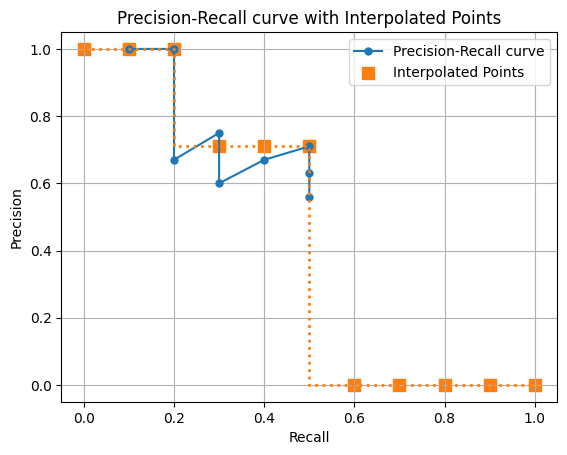
ポイントが11個あり、オレンジ色のラインの下の面積がAPになります。
もし複数の適合率(Precision)の値が同じ再現率(Recall)の値を持つ場合は、APの値には影響ないので簡略化のために一番適合率が高い行のみを残せばいいようです。
簡略した場合、AP値が同じかどうかも試してようと思います。
precision = [1.0, 1.0, 0.75, 0.67, 0.71]
recall = [0.1, 0.2, 0.3, 0.4, 0.5]
ap = draw_interp_pr_auc(precision,recall,11)11 Point Interpolation Average Precision (AP): 0.4664
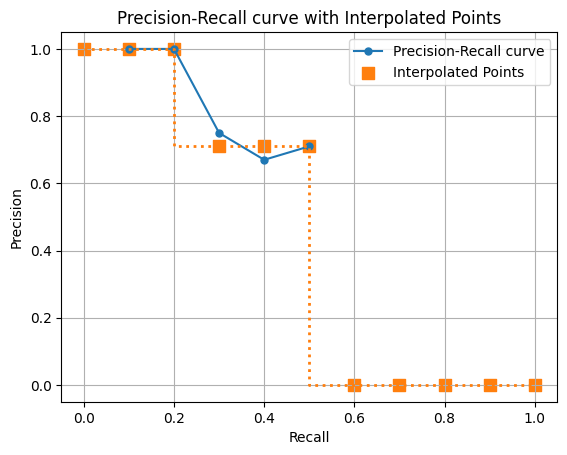
なんとAP値が等しくなりました。大量データの場合は計算量を下げることが出来そうですね。
101点補完APの計算と描画
順番は前後してしまいますが、PR-AUCの前に101点補完APを計算してみます。
precision = [1.0, 1.0, 0.67, 0.75, 0.60, 0.67, 0.71, 0.63, 0.56]
recall = [0.1, 0.2, 0.2, 0.3, 0.3, 0.4, 0.5, 0.5, 0.5]
ap = draw_interp_pr_auc(precision,recall,101)101 Point Interpolation Average Precision (AP): 0.4228
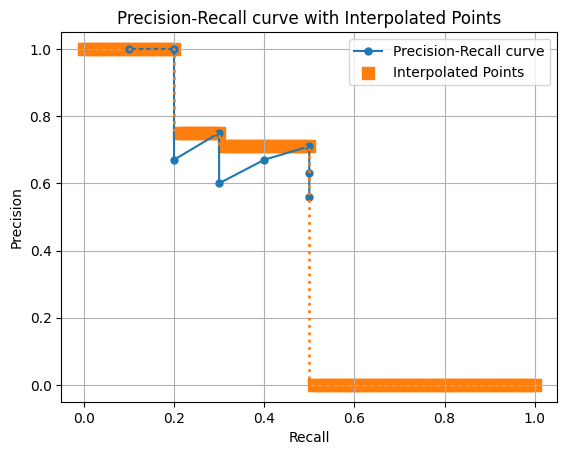
オレンジのポイントが101個あるので、ほぼ線みたいになりました 笑
APも11pointsの場合は0.4664でしたが、101pointsになると0.4228になりました。
PR-AUCによるAPの計算と描画
import numpy as np
import matplotlib.pyplot as plt
# データ
precision = [1.0, 1.0, 0.67, 0.75, 0.60, 0.67, 0.71, 0.63, 0.56]
recall = [0.1, 0.2, 0.2, 0.3, 0.3, 0.4, 0.5, 0.5, 0.5]
# AUC計算用のリストを作成
max_precision = np.maximum.accumulate(precision[::-1])[::-1]
new_recall=recall.copy()
# 足らない点を追加
if recall[0] != 0:
new_recall.insert(0, 0)
max_precision = np.insert(max_precision, 0, max_precision[0])
# PR曲線の描画
plt.plot(recall, precision, marker='o', markersize=5, label='Precision-Recall curve')
plt.scatter(new_recall, max_precision, color="#ff7f0e", marker='s',s=80,label="Max Precision")
plt.plot(new_recall, max_precision,linestyle='dotted', color="#ff7f0e", linewidth=2)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.legend()
plt.title('Precision-Recall Curve with Max Precision Points')
plt.show()
# APの計算
ap = np.sum(np.diff(new_recall) * max_precision[:-1])
print("PR-AUC Average Precision (AP):", ap)
PR-AUC Average Precision (AP): 0.41700000000000004
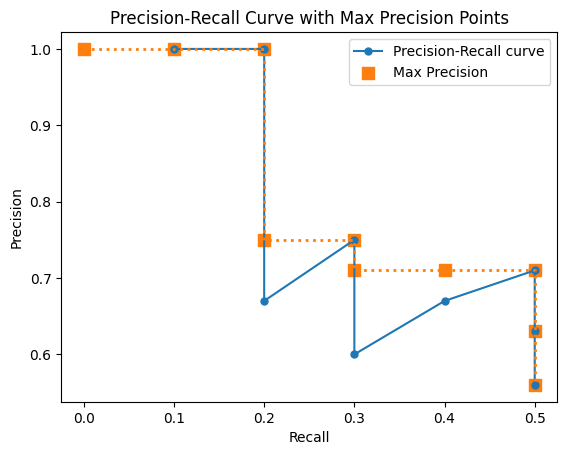
オレンジ色のラインの下の面積の合計になります。
AUC = 1* 0.1 + 1*0.1 + 0.75 * 0.1 + 0.2 * 0.71=0.417
になります。
※ 今回のサンプルデータだと、一番確信度が高い物体がTPだったためrecallの値が0.1から始まります。この場合、recallの0 ~ 0.1の間が空白になってしまうためそのまま計算していいものか悩んでいましたが、「How to calculate mAP for detection task for the PASCAL VOC Challenge?」を確認していたら補完してあげているみたいだったのでrecall=0、max_precision=max_precision[0]の値をAP計算用に追加しています。
(おまけ) precisionが0から始まる場合どういう見え方になるのか
下記のような結果があると仮定します。まさかの確信度が一番高いのにFPだった場合を想定しています。
過学習を起こしているとこのような状況が発生しやすいかも知れません。
| conf | TP or FP | Precision | Recall |
|---|---|---|---|
| 0.99 | FP | 0 / (0+1) = 0 | 0 / 10 = 0 |
| 0.80 | TP | 1 / (1+1) = 0.5 | 1 / 10 = 0.1 |
| 0.80 | TP | 2 / (2+1) = 0.66 | 2 / 10 = 0.2 |
| 0.3 | FP | 2 / (2+2) = 0.5 | 2 / 10 = 0.2 |
| 0.3 | FP | 2 / (2+3) = 0.4 | 2 / 10 = 0.2 |
precision = [0,0.5,0.66,0.5,0.4]
recall = [0,0.1,0.2,0.2,0.2]
ap = draw_interp_pr_auc(precision,recall,11)11 Point Interpolation Average Precision (AP): 0.1800
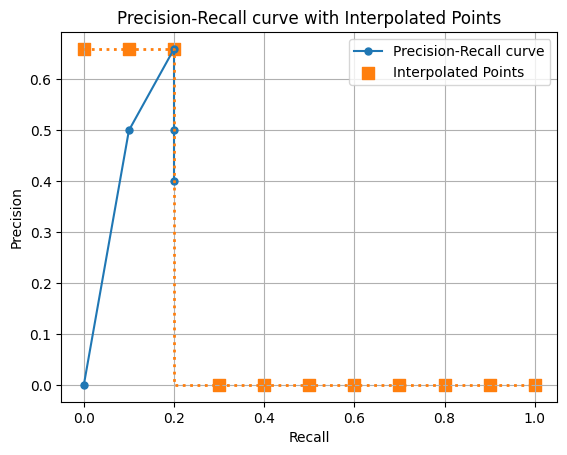
一応最初のprecisionが0の場合でも、precision=0.66で補完してくれるようです。
まとめ
物体検知の精度を検証するのに様々な手法があることが分かりました。
特にMS COCOの101点補完APが23年4月現在の主流なのであれば、私もこの方法でモデルの比較をしてみようかなと思いました。
ただし数字ばかりで確認していても何がどのように検知できなかったのかが分かりづらいので、そこは引き続き目視で確認していこうと思います 笑
次回はYOLOv8のモデルでdetectした結果の精度を実際にAPもしくはmAPで計算してみようと思います。

