前回の記事ではタイタニックのデータセットの欠損値処理をまとめていました。
今回は 2. 外れ値処理 (outlier processing)の作業をしようと思います。
外れ値処理に関してはKaggleの下記コードが参考になりました。
https://www.kaggle.com/code/nareshbhat/outlier-the-silent-killer
https://www.kaggle.com/code/aimack/how-to-handle-outliers
外れ値かどうかを判断するため、外れ値の検定を試してみた記事もあります。
それでは、外れ値の処理をしていきたいと思います。
タイタニックのデータセットの読み込み
import pandas as pd
import numpy as np
# タイタニックデータセットの訓練データを読み込み
df = pd.read_csv("/Users/hinomaruc/Desktop/notebooks/titanic/train.csv")正規性の確認
外れ値の検定に利用するSmirnov‐Grubbs TestやGeneralized Extreme Studentized Deviate (ESD) Testはおおよそ正規分布を仮定しているので、まずは各変数が正規分布に従っているか確認をしようと思います。
詳細はPythonで外れ値の検定を2種類試してみたに記載していますが、QQプロットというグラフを確認して正規分布に従っていそうか確認しようと思います。
せっかくなので正規性の検定の実行手順についてでも紹介されている正規性の検定も試してみようと思います。
下記2つのテストがあるようです。
・Kolmogorov-Smirnov test
・Shapiro-Wilk test (少ないサンプルのときに使用。versionによるかもしれませんが、scipyだと5000サンプル以上だとwarningがでました。
QQプロットで正規分布に従っているかどうか確認
# 描画設定
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_style("whitegrid")
from matplotlib import rcParams
rcParams['font.family'] = 'Hiragino Sans' # Macの場合
#rcParams['font.family'] = 'Meiryo' # Windowsの場合
#rcParams['font.family'] = 'VL PGothic' # Linuxの場合
rcParams['xtick.labelsize'] = 12 # x軸のラベルのフォントサイズ
rcParams['ytick.labelsize'] = 12 # y軸のラベルのフォントサイズ
rcParams['axes.labelsize'] = 18 # ラベルのフォントとサイズ
rcParams['figure.figsize'] = 18,8 # 画像サイズの変更(inch)# 正規分布に従うかどうかをQQプロットを描画して確認
from scipy import stats
CHK_COLUMNS=[
"Survived"
, "Pclass"
, "Age"
, "SibSp"
, "Parch"
, "Fare"
]
for i in CHK_COLUMNS:
print(i)
stats.probplot(df[i].dropna(), dist="norm", plot=plt)
plt.show()Survived
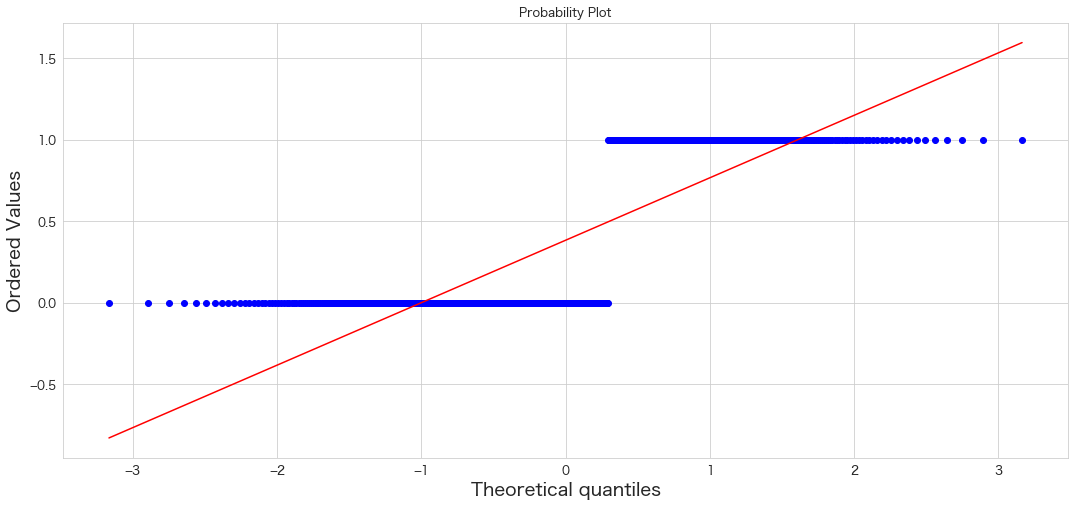
Pclass
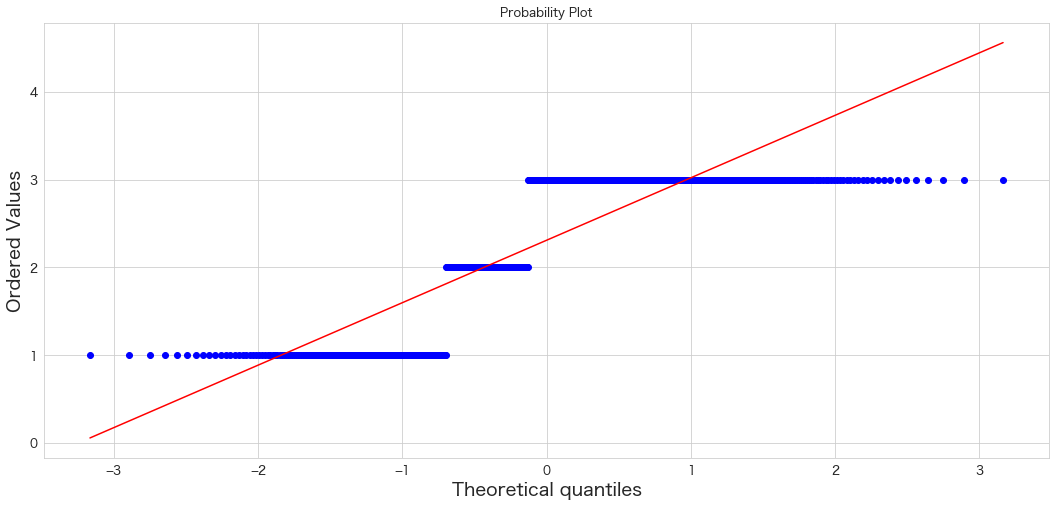
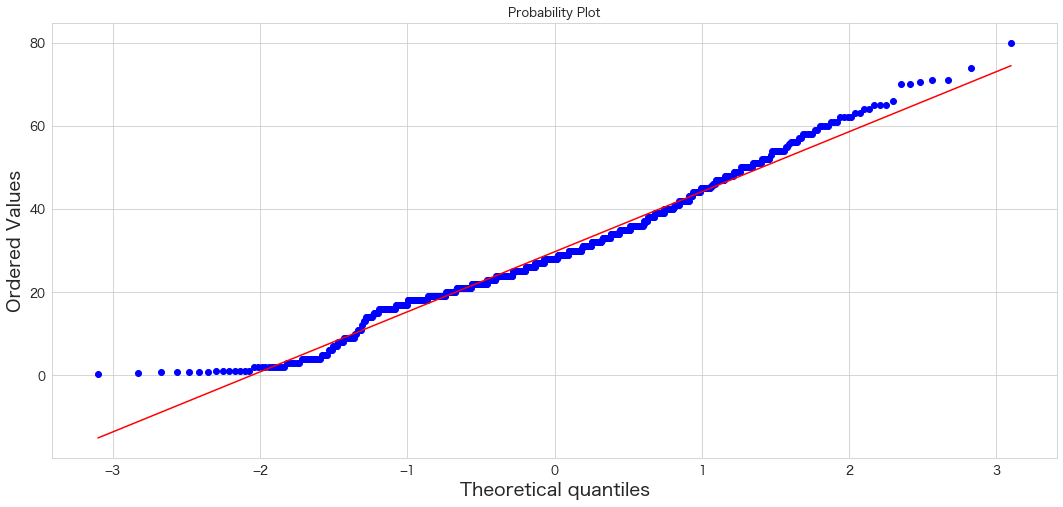
Age
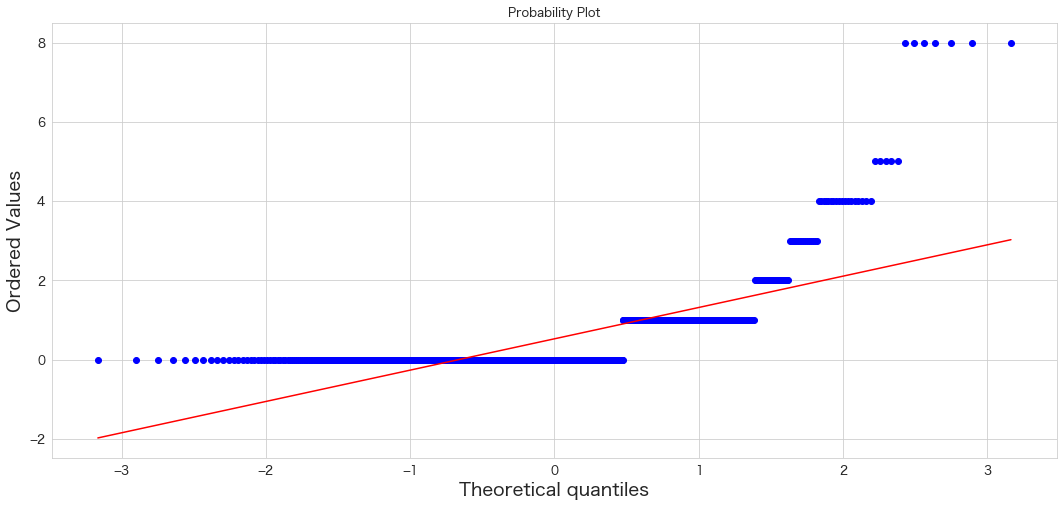
SibSp
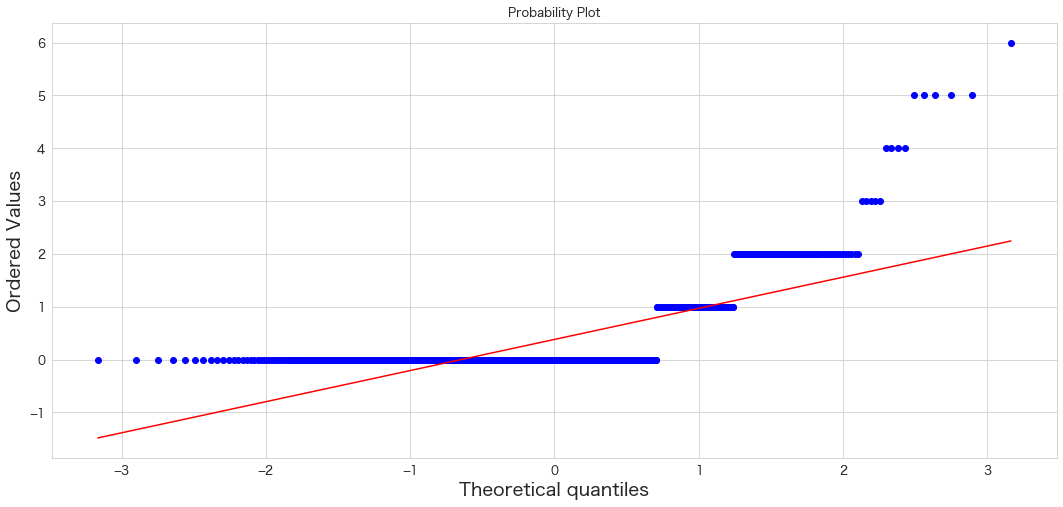
Parch
Fare
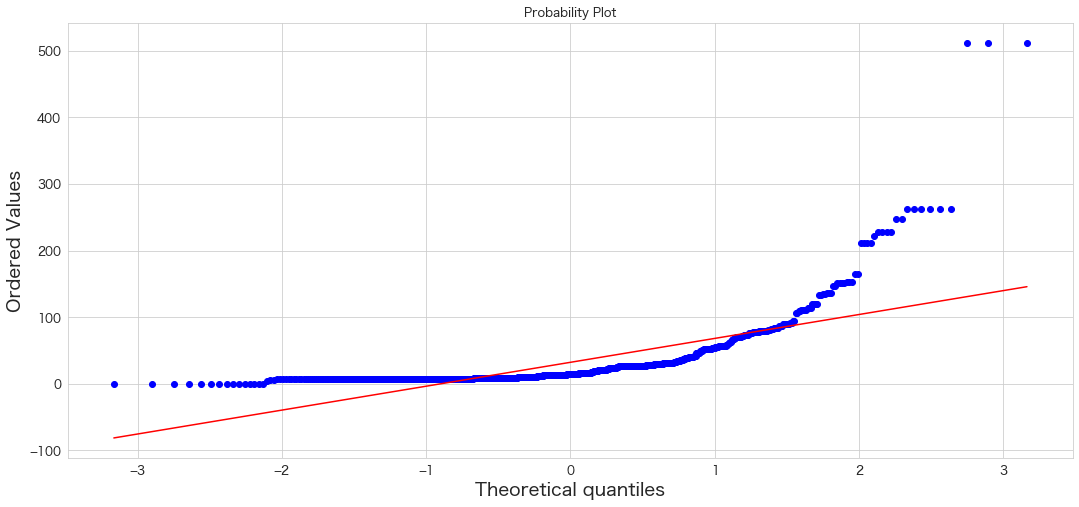
QQプロットは直線にプロットが沿っていると正規分布に従っているという解釈になるようです。
Ageだけおおよそ正規分布に従っているようです。
Kolmogorov-Smirnov testとShapiro-Wilk testでも確認
Ageがおおよそ正規分布に従っていそうなので、正規性テストをしてみようと思います。
# 正規分布かどうかのテスト
# Kolmogorov–Smirnov test
# H0=分布が正規分布である
from scipy import stats
stats.kstest(df["Age"].dropna(),"norm")
KstestResult(statistic=0.9650366565902186, pvalue=0.0)
# Shapiro–Wilk test
# H0=分布が正規分布である
stats.shapiro(df["Age"].dropna())
ShapiroResult(statistic=0.9814548492431641, pvalue=7.322165629375377e-08)
pvalue > 0.05ではないので、正規性テストだと正規分布ではないと結果になりました。QQプロットで確認することが大切ということがわかります。
正規性の確認後の手順まとめ
正規分布だった場合の処理 (if Normal distribution)
TitanicのデータセットですとAgeカラムのみが対象ですが、下記手順で外れ値を発見していきます。
- Smirnov‐Grubbs Test や generalized ESD testで外れ値の検定をする
- もしくは、ロバストZスコアが±3.5の範囲を外れる値を外れ値と定義
grabb's testを使う
# Grubb's test (max one sided)
#H0: there are no outliers in the data
#Ha: the maximum value is an outlier
def grubbs_test_onesided_max(Y):
import numpy as np
import scipy.stats as stats
# Significance level
alpha = 0.05
# Calculate G
Ymean = np.mean(Y)
s = np.std(Y, ddof=1) # use sample std
max_val = np.max(Y)
G_calculated = (max_val - Ymean) / s
# critical value of the t distribution with N-2 degrees of freedom and a significance level of α/(N).
N = len(Y)
t = stats.t.ppf(1 - (alpha / N), N - 2)
G_critical = (N - 1) / np.sqrt(N) * np.sqrt(np.square(t) / ((N - 2) + np.square(t)))
print("max_val = ", max_val)
print("G_calculated = ", G_calculated)
print("G_critical = ", G_critical)
if G_calculated > G_critical:
print("G_calculated > G_criticalなので帰無仮説は棄却され", max_val ,"は外れ値である")
else:
print("G_calculated < G_criticalなので帰無仮説は棄却されず", max_val ,"は外れ値であるとは言えない")grubbs_test_onesided_max(df["Age"].dropna().values)
max_val = 80.0
G_calculated = 3.4626986259776564
G_critical = 3.790080012280718
G_calculated < G_criticalなので帰無仮説は棄却されず 80.0 は外れ値であるとは言えない
generalized ESD testを使う
grubb's testよりgeneralized ESD testの方が複数の外れ値検定に使えるので適していそうです。
# Generalized ESD test (https://www.itl.nist.gov/div898/handbook/eda/section3/eda35h3.htm)
# H0: There are no outliers in the data set
# Ha: There are up to r outliers in the data set
# arguments Y:numpy.ndarray、r:iteration num
def generalized_esd_test(Y,r):
import numpy as np
import scipy.stats as stats
# deepcopyしておく
from copy import deepcopy
X = deepcopy(Y)
# maximum iteration num
r = r
# Significance level
alpha = 0.05
# sample size
N = len(X)
# Calculate G
for i in range(1, r + 1):
print("i = ",i)
Xmean = np.mean(X)
s = np.std(X, ddof=1) # use sample std
max_diviation = max(abs(X - Xmean))
max_diviation_idx = np.argmax(abs(X - Xmean))
possible_outlier = Y[max_diviation_idx]
# G calculatedを計算
G_calculated = max_diviation / s
print("possible_outlier = ",possible_outlier,"(idx = ",str(max_diviation_idx) + ")")
# critical value of the t distribution with N-i-1 degrees of freedom and a significance level of α/2(N-i+1).
t = stats.t.ppf(1 - (alpha / (2 * (N - i + 1))), N - i - 1)
print("N=",N - i + 1)
print("t=",t,"degree of freedom=",N - i - 1)
# G criticalを計算
G_critical = (N - i) * t / np.sqrt((N - i - 1 + np.square(t)) * (N - i + 1))
print("G_calculated = ", G_calculated)
print("G_critical = ", G_critical)
if G_calculated > G_critical:
print("G_calculated > G_criticalなので帰無仮説は棄却され外れ値は存在する *")
else:
print("G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない")
# 外れ値と思われる値を削除し再度検定をする
X = np.delete(X,max_diviation_idx,0)
print("\n")generalized_esd_test(df["Age"].dropna().values,100)
i = 1
possible_outlier = 80.0 (idx = 498)
N= 714
t= 3.999783237713572 degree of freedom= 712
G_calculated = 3.4626986259776564
G_critical = 3.9555939826790274
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 2
possible_outlier = 4.0 (idx = 678)
N= 713
t= 3.999477386217029 degree of freedom= 711
G_calculated = 3.078404668802844
G_critical = 3.9552370525253457
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 3
possible_outlier = 71.0 (idx = 74)
N= 712
t= 3.999171112061637 degree of freedom= 710
G_calculated = 2.891911703546862
G_critical = 3.9548795703056583
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 4
possible_outlier = 55.0 (idx = 392)
N= 711
t= 3.9988644140998093 degree of freedom= 709
G_calculated = 2.9111378503318672
G_critical = 3.95452153436388
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 5
possible_outlier = 21.0 (idx = 90)
N= 710
t= 3.9985572911789533 degree of freedom= 708
G_calculated = 2.8954853105989664
G_critical = 3.9541629430362133
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 6
possible_outlier = 25.0 (idx = 527)
N= 709
t= 3.998249742141604 degree of freedom= 707
G_calculated = 2.8793800856041902
G_critical = 3.9538037946512676
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 7
possible_outlier = 35.0 (idx = 587)
N= 708
t= 3.9979417658255585 degree of freedom= 706
G_calculated = 2.8984548012161757
G_critical = 3.953444087530165
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 8
possible_outlier = 66.0 (idx = 25)
N= 707
t= 3.9976333610640142 degree of freedom= 705
G_calculated = 2.6313045639511925
G_critical = 3.953083819986654
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 9
possible_outlier = 29.0 (idx = 39)
N= 706
t= 3.997324526685705 degree of freedom= 704
G_calculated = 2.5742351258054215
G_critical = 3.9527229903272274
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 10
possible_outlier = 63.0 (idx = 221)
N= 705
t= 3.997015261514277 degree of freedom= 703
G_calculated = 2.5882679256657513
G_critical = 3.95236159685049
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 11
possible_outlier = 52.0 (idx = 361)
N= 704
t= 3.996705564369187 degree of freedom= 702
G_calculated = 2.6025327956320043
G_critical = 3.951999637848016
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 12
possible_outlier = 17.0 (idx = 346)
N= 703
t= 3.996395434062812 degree of freedom= 701
G_calculated = 2.5441949153929966
G_critical = 3.9516371116015274
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 13
possible_outlier = 45.0 (idx = 425)
N= 702
t= 3.996084869405895 degree of freedom= 700
G_calculated = 2.557840511772124
G_critical = 3.9512740163881452
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 14
possible_outlier = 35.0 (idx = 217)
N= 701
t= 3.9957738692023828 degree of freedom= 699
G_calculated = 2.4982885702077184
G_critical = 3.950910350475372
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 15
possible_outlier = 23.0 (idx = 377)
N= 700
t= 3.9954624322518404 degree of freedom= 698
G_calculated = 2.511306855235973
G_critical = 3.9505461121234102
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 16
possible_outlier = 24.0 (idx = 199)
N= 699
t= 3.9951505573480874 degree of freedom= 697
G_calculated = 2.4505517764013174
G_critical = 3.9501812995838206
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 17
possible_outlier = 9.0 (idx = 429)
N= 698
t= 3.994838243280854 degree of freedom= 696
G_calculated = 2.462937042940008
G_critical = 3.9498159111011044
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 18
possible_outlier = 27.0 (idx = 438)
N= 697
t= 3.9945254888351673 degree of freedom= 695
G_calculated = 2.4755120607107415
G_critical = 3.949449944912085
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 19
possible_outlier = 39.0 (idx = 645)
N= 696
t= 3.994212292789997 degree of freedom= 694
G_calculated = 2.4882817249078317
G_critical = 3.9490833992445813
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 20
possible_outlier = 1.0 (idx = 132)
N= 695
t= 3.993898653919909 degree of freedom= 693
G_calculated = 2.4261735959609085
G_critical = 3.948716272318986
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 21
possible_outlier = 54.0 (idx = 254)
N= 694
t= 3.993584570994465 degree of freedom= 692
G_calculated = 2.4382958727453263
G_critical = 3.9483485623476553
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 22
possible_outlier = 30.0 (idx = 478)
N= 693
t= 3.9932700427776204 degree of freedom= 691
G_calculated = 2.450601733924487
G_critical = 3.9479802675343176
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 23
possible_outlier = 25.0 (idx = 284)
N= 692
t= 3.9929550680293757 degree of freedom= 690
G_calculated = 2.387204801652519
G_critical = 3.947611386075636
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 24
possible_outlier = 19.0 (idx = 448)
N= 691
t= 3.9926396455021944 degree of freedom= 689
G_calculated = 2.3988556870656685
G_critical = 3.947241916157731
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 25
possible_outlier = 58.0 (idx = 520)
N= 690
t= 3.9923237739463784 degree of freedom= 688
G_calculated = 2.41067888567203
G_critical = 3.946871855961351
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 26
possible_outlier = 43.0 (idx = 528)
N= 689
t= 3.9920074521050073 degree of freedom= 687
G_calculated = 2.422678687196788
G_critical = 3.9465012036569584
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 27
possible_outlier = 46.0 (idx = 71)
N= 688
t= 3.9916906787163304 degree of freedom= 686
G_calculated = 2.357900927060036
G_critical = 3.946129957407021
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 28
possible_outlier = 22.0 (idx = 181)
N= 687
t= 3.991373452513177 degree of freedom= 685
G_calculated = 2.369234145475613
G_critical = 3.945758115365416
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 29
possible_outlier = 58.0 (idx = 10)
N= 686
t= 3.9910557722238655 degree of freedom= 684
G_calculated = 2.303254501256145
G_critical = 3.945385675678287
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 30
possible_outlier = 40.0 (idx = 149)
N= 685
t= 3.9907376365701297 degree of freedom= 683
G_calculated = 2.3139232737964557
G_critical = 3.945012636482019
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 31
possible_outlier = 29.0 (idx = 206)
N= 684
t= 3.9904190442695064 degree of freedom= 682
G_calculated = 2.324741726981293
G_critical = 3.9446389959055144
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 32
possible_outlier = 47.0 (idx = 370)
N= 683
t= 3.99009999403402 degree of freedom= 681
G_calculated = 2.3357133938377737
G_critical = 3.9442647520689107
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 33
possible_outlier = 61.0 (idx = 494)
N= 682
t= 3.9897804845696037 degree of freedom= 680
G_calculated = 2.346841925254589
G_critical = 3.9438899030829844
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 34
possible_outlier = 37.0 (idx = 470)
N= 681
t= 3.9894605145762734 degree of freedom= 679
G_calculated = 2.2793853838286444
G_critical = 3.943514447049302
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 35
possible_outlier = 23.0 (idx = 584)
N= 680
t= 3.9891400827512284 degree of freedom= 678
G_calculated = 2.289835850562417
G_critical = 3.943138382063194
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 36
possible_outlier = 9.0 (idx = 133)
N= 679
t= 3.9888191877824073 degree of freedom= 677
G_calculated = 2.221192039308914
G_critical = 3.942761706207495
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 37
possible_outlier = 25.0 (idx = 355)
N= 678
t= 3.9884978283552677 degree of freedom= 676
G_calculated = 2.230971106397375
G_critical = 3.942384417559079
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 38
possible_outlier = 35.0 (idx = 483)
N= 677
t= 3.9881760031478155 degree of freedom= 675
G_calculated = 2.2408805180919487
G_critical = 3.942006514184027
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 39
possible_outlier = 23.0 (idx = 665)
N= 676
t= 3.9878537108337153 degree of freedom= 674
G_calculated = 2.25092319595566
G_critical = 3.941627994140605
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 40
possible_outlier = 27.0 (idx = 117)
N= 675
t= 3.9875309500795306 degree of freedom= 673
G_calculated = 2.221008172763438
G_critical = 3.94124885547658
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 41
possible_outlier = 28.0 (idx = 603)
N= 674
t= 3.9872077195485485 degree of freedom= 672
G_calculated = 2.1988959016534033
G_critical = 3.9408690962328783
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 42
possible_outlier = 14.0 (idx = 13)
N= 673
t= 3.986884017895129 degree of freedom= 671
G_calculated = 2.193644628203823
G_critical = 3.940488714438114
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 43
possible_outlier = 34.0 (idx = 369)
N= 672
t= 3.9865598437706993 degree of freedom= 670
G_calculated = 2.20318804614288
G_critical = 3.940107708114341
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 44
possible_outlier = 24.0 (idx = 564)
N= 671
t= 3.986235195819574 degree of freedom= 669
G_calculated = 2.1943520453747536
G_critical = 3.939726075272998
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 45
possible_outlier = 45.0 (idx = 353)
N= 670
t= 3.9859100726805825 degree of freedom= 668
G_calculated = 2.1974242007647864
G_critical = 3.9393438139164494
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 46
possible_outlier = 35.0 (idx = 476)
N= 669
t= 3.9855844729872496 degree of freedom= 667
G_calculated = 2.2070548064778417
G_critical = 3.9389609220381336
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 47
possible_outlier = 21.0 (idx = 55)
N= 668
t= 3.985258395365088 degree of freedom= 666
G_calculated = 2.210267206834921
G_critical = 3.938577397619925
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 48
possible_outlier = 5.0 (idx = 619)
N= 667
t= 3.984931838436839 degree of freedom= 665
G_calculated = 2.2200783632778047
G_critical = 3.9381932386371616
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 49
possible_outlier = 28.0 (idx = 226)
N= 666
t= 3.9846048008168773 degree of freedom= 664
G_calculated = 2.2226135745633253
G_critical = 3.93780844305322
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 50
possible_outlier = 55.5 (idx = 123)
N= 665
t= 3.984277281115008 degree of freedom= 663
G_calculated = 2.2259977084637446
G_critical = 3.937423008823151
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 51
possible_outlier = 30.0 (idx = 127)
N= 664
t= 3.983949277933772 degree of freedom= 662
G_calculated = 2.236042165050184
G_critical = 3.9370369338910507
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 52
possible_outlier = 9.0 (idx = 133)
N= 663
t= 3.983620789871513 degree of freedom= 661
G_calculated = 2.2462238711911198
G_critical = 3.9366502161929953
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 53
possible_outlier = 23.0 (idx = 282)
N= 662
t= 3.9832918155182546 degree of freedom= 660
G_calculated = 2.2565459813095283
G_critical = 3.936262853653029
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 54
possible_outlier = 28.0 (idx = 285)
N= 661
t= 3.982962353460204 degree of freedom= 659
G_calculated = 2.267011752266979
G_critical = 3.9358748441874867
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 55
possible_outlier = 25.0 (idx = 579)
N= 660
t= 3.9826324022756374 degree of freedom= 658
G_calculated = 2.2776245476807944
G_critical = 3.935486185700989
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 56
possible_outlier = 16.0 (idx = 610)
N= 659
t= 3.9823019605372534 degree of freedom= 657
G_calculated = 2.288387842465697
G_critical = 3.9350968760886897
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 57
possible_outlier = 2.0 (idx = 6)
N= 658
t= 3.981971026811647 degree of freedom= 656
G_calculated = 2.214929406980869
G_critical = 3.934706913235736
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 58
possible_outlier = 39.0 (idx = 12)
N= 657
t= 3.9816395996588003 degree of freedom= 655
G_calculated = 2.2249470920643737
G_critical = 3.934316295016746
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 59
possible_outlier = 38.0 (idx = 84)
N= 656
t= 3.9813076776336986 degree of freedom= 654
G_calculated = 2.235101981832808
G_critical = 3.9339250192973414
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 60
possible_outlier = 9.0 (idx = 145)
N= 655
t= 3.9809752592829826 degree of freedom= 653
G_calculated = 2.2453972371411317
G_critical = 3.933533083930884
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 61
possible_outlier = 58.0 (idx = 216)
N= 654
t= 3.980642343148702 degree of freedom= 652
G_calculated = 2.255836121736949
G_critical = 3.9331404867620714
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 62
possible_outlier = 30.0 (idx = 246)
N= 653
t= 3.9803089277656785 degree of freedom= 651
G_calculated = 2.2664220066072676
G_critical = 3.9327472256243556
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 63
possible_outlier = 50.0 (idx = 347)
N= 652
t= 3.9799750116617205 degree of freedom= 650
G_calculated = 2.2771583745518145
G_critical = 3.9323532983401255
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 64
possible_outlier = 22.0 (idx = 381)
N= 651
t= 3.9796405933599415 degree of freedom= 649
G_calculated = 2.2880488249970146
G_critical = 3.931958702722907
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 65
possible_outlier = 39.0 (idx = 460)
N= 650
t= 3.9793056713754487 degree of freedom= 648
G_calculated = 2.299097079065728
G_critical = 3.931563436574142
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 66
possible_outlier = 23.0 (idx = 600)
N= 649
t= 3.9789702442169568 degree of freedom= 647
G_calculated = 2.3103069849189697
G_critical = 3.9311674976847097
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 67
possible_outlier = 21.0 (idx = 28)
N= 648
t= 3.9786343103870094 degree of freedom= 646
G_calculated = 2.2345841458524522
G_critical = 3.9307708838351085
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 68
possible_outlier = 61.0 (idx = 136)
N= 647
t= 3.978297868381481 degree of freedom= 645
G_calculated = 2.245001057889017
G_critical = 3.930373592794945
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 69
possible_outlier = 59.0 (idx = 187)
N= 646
t= 3.9779609166897973 degree of freedom= 644
G_calculated = 2.255565064846227
G_critical = 3.9299756223231124
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 70
possible_outlier = 26.0 (idx = 249)
N= 645
t= 3.9776234537937536 degree of freedom= 643
G_calculated = 2.2662796614586846
G_critical = 3.929576970166619
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 71
possible_outlier = 45.5 (idx = 266)
N= 644
t= 3.977285478169829 degree of freedom= 642
G_calculated = 2.277148459815918
G_critical = 3.9291776340627864
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 72
possible_outlier = 60.0 (idx = 293)
N= 643
t= 3.976946988285918 degree of freedom= 641
G_calculated = 2.288175194478235
G_critical = 3.9287776117360615
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 73
possible_outlier = 54.0 (idx = 5)
N= 642
t= 3.9766079826050404 degree of freedom= 640
G_calculated = 2.2291034707997412
G_critical = 3.928376900901566
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 74
possible_outlier = 47.0 (idx = 85)
N= 641
t= 3.976268459581386 degree of freedom= 639
G_calculated = 2.23954959840261
G_critical = 3.9279754992612403
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 75
possible_outlier = 16.0 (idx = 177)
N= 640
t= 3.9759284176647154 degree of freedom= 638
G_calculated = 2.2501440187748436
G_critical = 3.927573404508062
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 76
possible_outlier = 45.0 (idx = 222)
N= 639
t= 3.9755878552950294 degree of freedom= 637
G_calculated = 2.260890274046948
G_critical = 3.927170614320862
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 77
possible_outlier = 42.0 (idx = 345)
N= 638
t= 3.975246770907657 degree of freedom= 636
G_calculated = 2.2717920259414215
G_critical = 3.9267671263692
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 78
possible_outlier = 4.0 (idx = 357)
N= 637
t= 3.974905162929331 degree of freedom= 635
G_calculated = 2.2828530610146864
G_critical = 3.9263629383095484
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 79
possible_outlier = 26.0 (idx = 405)
N= 636
t= 3.9745630297811894 degree of freedom= 634
G_calculated = 2.2940772961826297
G_critical = 3.9259580477881406
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 80
possible_outlier = 15.0 (idx = 546)
N= 635
t= 3.974220369876243 degree of freedom= 633
G_calculated = 2.3054687845480206
G_critical = 3.9255524524385046
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 81
possible_outlier = 27.0 (idx = 7)
N= 634
t= 3.9738771816196206 degree of freedom= 632
G_calculated = 2.240262165223447
G_critical = 3.9251461498816558
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 82
possible_outlier = 29.0 (idx = 39)
N= 633
t= 3.9735334634108774 degree of freedom= 631
G_calculated = 2.250983662689736
G_critical = 3.9247391377282876
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 83
possible_outlier = 9.0 (idx = 118)
N= 632
t= 3.9731892136421596 degree of freedom= 630
G_calculated = 2.2618606277080033
G_critical = 3.9243314135769665
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 84
possible_outlier = 40.5 (idx = 124)
N= 631
t= 3.972844430697086 degree of freedom= 629
G_calculated = 2.2728968542395607
G_critical = 3.9239229750130127
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 85
possible_outlier = 17.0 (idx = 311)
N= 630
t= 3.9724991129523652 degree of freedom= 628
G_calculated = 2.284096267142741
G_critical = 3.923513819610027
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 86
possible_outlier = 7.0 (idx = 424)
N= 629
t= 3.972153258778723 degree of freedom= 627
G_calculated = 2.2954629280371437
G_critical = 3.923103944930742
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 87
possible_outlier = 44.0 (idx = 475)
N= 628
t= 3.971806866537733 degree of freedom= 626
G_calculated = 2.307001041492208
G_critical = 3.9226933485239304
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 88
possible_outlier = 50.0 (idx = 521)
N= 627
t= 3.9714599345841224 degree of freedom= 625
G_calculated = 2.3187149615615392
G_critical = 3.922282027926588
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 89
possible_outlier = 70.0 (idx = 592)
N= 626
t= 3.9711124612660185 degree of freedom= 624
G_calculated = 2.3306091986860378
G_critical = 3.921869980664134
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 90
possible_outlier = 33.0 (idx = 606)
N= 625
t= 3.970764444921807 degree of freedom= 623
G_calculated = 2.3426884269907013
G_critical = 3.921457204247342
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 91
possible_outlier = 21.0 (idx = 391)
N= 624
t= 3.970415883885145 degree of freedom= 622
G_calculated = 2.265794627323651
G_critical = 3.9210436961771307
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 92
possible_outlier = 19.0 (idx = 34)
N= 623
t= 3.9700667764791144 degree of freedom= 621
G_calculated = 2.2645723128019624
G_critical = 3.9206294539388926
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 93
possible_outlier = 28.0 (idx = 159)
N= 622
t= 3.969717121021226 degree of freedom= 620
G_calculated = 2.275805433247651
G_critical = 3.92021447500727
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 94
possible_outlier = 17.0 (idx = 311)
N= 621
t= 3.969366915820979 degree of freedom= 619
G_calculated = 2.287207440606989
G_critical = 3.919798756843768
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 95
possible_outlier = 18.0 (idx = 535)
N= 620
t= 3.969016159179446 degree of freedom= 618
G_calculated = 2.298782609684593
G_critical = 3.9193822968963126
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 96
possible_outlier = 21.0 (idx = 493)
N= 619
t= 3.9686648493895524 degree of freedom= 617
G_calculated = 2.214618166720857
G_critical = 3.918965092599473
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 97
possible_outlier = 18.0 (idx = 516)
N= 618
t= 3.968312984737016 degree of freedom= 616
G_calculated = 2.2252682557758834
G_critical = 3.9185471413753317
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 98
possible_outlier = 45.0 (idx = 561)
N= 617
t= 3.967960563499946 degree of freedom= 615
G_calculated = 2.2360735337856017
G_critical = 3.9181284406330468
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 99
possible_outlier = 27.0 (idx = 178)
N= 616
t= 3.967607583948444 degree of freedom= 614
G_calculated = 2.2080463865610183
G_critical = 3.9177089877684375
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
i = 100
possible_outlier = 36.0 (idx = 310)
N= 615
t= 3.967254044343545 degree of freedom= 613
G_calculated = 2.218664082829254
G_critical = 3.917288780162909
G_calculated < G_criticalなので帰無仮説は棄却されず外れ値は存在するとは言えない
r=100でtestしてみましたが、外れ値は存在するとは言えないという結果になりました。
ロバストZスコアを使う (Modified Zscoreとも言われるようです)
通常のZスコアは平均値(mean)と標準偏差(standard deviation)を利用するので外れ値の影響を受けやすいですが、ロバストZスコアでは中央値(median)と中央絶対偏差(median absolute deviation)を利用するので外れ値の影響を軽減できるようです。
※ 中央絶対偏差を使う以外にもNormalized IQRなどを使う方法もあるようです。
# ロバストZスコア基準での外れ値の検出
# MAD is scaled. please check below link for reference
# https://stats.stackexchange.com/questions/523865/calculating-robust-z-scores-with-median-and-mad
def outlier_detector_robust_zscore(Y):
import numpy as np
import scipy.stats as stats
x = Y
x = x[~np.isnan(x)]
median = np.median(x)
MAD = stats.median_abs_deviation(x, scale='normal') # scale to fit sample standard deviation
print("median =",median,"MAD =",MAD)
outliers_list=[]
for val in x:
robust_zscore = 0.6745 * (val - median) / MAD
if np.abs(robust_zscore) > 3.5:
outliers_list.append(val)
if(len(outliers_list) == 0):
return 'no possible outliers'
else:
return print(outliers_list)outlier_detector_robust_zscore(df["Age"].dropna())
median = 28.0 MAD = 13.343419966550417
'no possible outliers'
正規分布ではない場合の処理 (if Skewed distribution)
QQプロットを確認する限り、SibSp・Parch・Fareに外れ値が存在していそうです。
その場合IQRで外れ値かどうかを判断できるようです。
- Q1 – 1.5 x IQR より小さい値、Q3 + 1.5 x IQR より大きい値を外れ値と定義
IQRを使う
# IQRでの外れ値検出を試す
def outlier_detector_iqr(Y):
import numpy as np
q1 = np.quantile(Y, 0.25)
q3 = np.quantile(Y,0.75)
IQR = q3 - q1
print("q1 =",q1,"q3 =",q3)
lower_bound = q1 - 1.5 * IQR
upper_bound = q3 + 1.5 * IQR
print("lower_bound =",lower_bound,"upper_bound =",upper_bound)
outliers_list=[]
for val in Y:
if val < lower_bound:
outliers_list.append(val)
elif val > upper_bound:
outliers_list.append(val)
if (len(outliers_list) == 0):
return 'no possible outliers'
else:
return print(outliers_list)outlier_detector_iqr(df["Fare"])
q1 = 7.9104 q3 = 31.0
lower_bound = -26.724 upper_bound = 65.6344
[71.2833, 263.0, 146.5208, 82.1708, 76.7292, 80.0, 83.475, 73.5, 263.0, 77.2875, 247.5208, 73.5, 77.2875, 79.2, 66.6, 69.55, 69.55, 146.5208, 69.55, 113.275, 76.2917, 90.0, 83.475, 90.0, 79.2, 86.5, 512.3292, 79.65, 153.4625, 135.6333, 77.9583, 78.85, 91.0792, 151.55, 247.5208, 151.55, 110.8833, 108.9, 83.1583, 262.375, 164.8667, 134.5, 69.55, 135.6333, 153.4625, 133.65, 66.6, 134.5, 263.0, 75.25, 69.3, 135.6333, 82.1708, 211.5, 227.525, 73.5, 120.0, 113.275, 90.0, 120.0, 263.0, 81.8583, 89.1042, 91.0792, 90.0, 78.2667, 151.55, 86.5, 108.9, 93.5, 221.7792, 106.425, 71.0, 106.425, 110.8833, 227.525, 79.65, 110.8833, 79.65, 79.2, 78.2667, 153.4625, 77.9583, 69.3, 76.7292, 73.5, 113.275, 133.65, 73.5, 512.3292, 76.7292, 211.3375, 110.8833, 227.525, 151.55, 227.525, 211.3375, 512.3292, 78.85, 262.375, 71.0, 86.5, 120.0, 77.9583, 211.3375, 79.2, 69.55, 120.0, 93.5, 80.0, 83.1583, 69.55, 89.1042, 164.8667, 69.55, 83.1583]
outlier_detector_iqr(df["SibSp"])
q1 = 0.0 q3 = 1.0
lower_bound = -1.5 upper_bound = 2.5
[3, 4, 3, 3, 4, 5, 3, 4, 5, 3, 3, 4, 8, 4, 4, 3, 8, 4, 8, 3, 4, 4, 4, 4, 8, 3, 3, 5, 3, 5, 3, 4, 4, 3, 3, 5, 4, 3, 4, 8, 4, 3, 4, 8, 4, 8]
outlier_detector_iqr(df["Parch"])
q1 = 0.0 q3 = 0.0
lower_bound = 0.0 upper_bound = 0.0
[1, 2, 1, 5, 1, 1, 5, 2, 2, 1, 1, 2, 2, 2, 1, 2, 2, 2, 3, 2, 2, 1, 1, 1, 1, 2, 1, 1, 2, 2, 1, 2, 2, 2, 1, 2, 1, 1, 2, 1, 4, 1, 1, 1, 1, 2, 2, 1, 2, 1, 1, 1, 2, 1, 1, 2, 2, 2, 1, 1, 2, 2, 1, 2, 1, 1, 1, 1, 1, 1, 1, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1, 1, 1, 1, 2, 1, 1, 1, 4, 1, 1, 2, 2, 2, 2, 2, 1, 1, 1, 2, 2, 1, 1, 2, 2, 3, 4, 1, 2, 1, 1, 2, 1, 2, 1, 2, 1, 1, 2, 2, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 1, 1, 2, 1, 4, 1, 1, 2, 1, 2, 1, 1, 2, 5, 2, 1, 1, 1, 2, 1, 5, 2, 1, 1, 1, 2, 1, 6, 1, 2, 1, 2, 1, 1, 1, 1, 1, 1, 1, 3, 2, 1, 1, 1, 1, 2, 1, 2, 3, 1, 2, 1, 2, 2, 1, 1, 2, 1, 2, 1, 2, 1, 1, 1, 2, 1, 1, 2, 1, 2, 1, 1, 1, 1, 3, 2, 1, 1, 1, 1, 5, 2]
(正規分布・傾斜分布どちらでも可) パーセンタイルで外れ値かどうかの閾値を定義
汎用的に使えるのがパーセンタイルのようです。
- 1パーセンタイルより小さい値、99パーセンタイルより大きい値を外れ値と定義
パーセンタイルを使う
# パーセンタイルで外れ値を検出する
def outlier_detector_percentile(Y):
import numpy as np
pct_001 = np.quantile(Y, 0.01)
pct_099 = np.quantile(Y,0.99)
print("pct_001 =",pct_001,"pct_099 =",pct_099)
lower_bound = pct_001
upper_bound = pct_099
print("lower_bound =",lower_bound,"upper_bound =",upper_bound)
outliers_list=[]
for val in Y:
if val < lower_bound:
outliers_list.append(val)
elif val > upper_bound:
outliers_list.append(val)
if (len(outliers_list) == 0):
return 'no possible outliers'
else:
return print(outliers_list)outlier_detector_percentile(df["Fare"])
pct_001 = 0.0 pct_099 = 249.00622000000035
lower_bound = 0.0 upper_bound = 249.00622000000035
[263.0, 263.0, 512.3292, 262.375, 263.0, 263.0, 512.3292, 512.3292, 262.375]
outlier_detector_percentile(df["SibSp"])
pct_001 = 0.0 pct_099 = 5.0
lower_bound = 0.0 upper_bound = 5.0
[8, 8, 8, 8, 8, 8, 8]
outlier_detector_percentile(df["Parch"])
pct_001 = 0.0 pct_099 = 4.0
lower_bound = 0.0 upper_bound = 4.0
[5, 5, 5, 5, 6, 5]
percentileの方がIQRより外れ値の基準が厳しそうです。
より扱いやすいのはパーセンタイルですかね。
外れ値の扱いを検討する
Ageの扱い
外れ値が存在しないようなのでそのまま
SibSp・Parch・Fareの扱い
外れ値と検出されても間違ったデータではないのでそのまま。
同行家族が多く、運賃も人数分合算されたものが入ってきているようだった。
確認内容
# パーセンタイルで外れ値という結果になるデータを表示
df.loc[(df["Fare"] > np.quantile(df["Fare"], 0.99)) | (df["Fare"] < np.quantile(df["Fare"], 0.01) )]| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 27 | 28 | 0 | 1 | Fortune, Mr. Charles Alexander | male | 19.0 | 3 | 2 | 19950 | 263.0000 | C23 C25 C27 | S |
| 88 | 89 | 1 | 1 | Fortune, Miss. Mabel Helen | female | 23.0 | 3 | 2 | 19950 | 263.0000 | C23 C25 C27 | S |
| 258 | 259 | 1 | 1 | Ward, Miss. Anna | female | 35.0 | 0 | 0 | PC 17755 | 512.3292 | NaN | C |
| 311 | 312 | 1 | 1 | Ryerson, Miss. Emily Borie | female | 18.0 | 2 | 2 | PC 17608 | 262.3750 | B57 B59 B63 B66 | C |
| 341 | 342 | 1 | 1 | Fortune, Miss. Alice Elizabeth | female | 24.0 | 3 | 2 | 19950 | 263.0000 | C23 C25 C27 | S |
| 438 | 439 | 0 | 1 | Fortune, Mr. Mark | male | 64.0 | 1 | 4 | 19950 | 263.0000 | C23 C25 C27 | S |
| 679 | 680 | 1 | 1 | Cardeza, Mr. Thomas Drake Martinez | male | 36.0 | 0 | 1 | PC 17755 | 512.3292 | B51 B53 B55 | C |
| 737 | 738 | 1 | 1 | Lesurer, Mr. Gustave J | male | 35.0 | 0 | 0 | PC 17755 | 512.3292 | B101 | C |
| 742 | 743 | 1 | 1 | Ryerson, Miss. Susan Parker "Suzette" | female | 21.0 | 2 | 2 | PC 17608 | 262.3750 | B57 B59 B63 B66 | C |
同じ家族は同じチケット番号や運賃になっているようです。
人数が多いFortune家を詳しく見ていきます。
# チケット番号が19950を表示
df.loc[(df["Ticket"] == '19950')]| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 27 | 28 | 0 | 1 | Fortune, Mr. Charles Alexander | male | 19.0 | 3 | 2 | 19950 | 263.0 | C23 C25 C27 | S |
| 88 | 89 | 1 | 1 | Fortune, Miss. Mabel Helen | female | 23.0 | 3 | 2 | 19950 | 263.0 | C23 C25 C27 | S |
| 341 | 342 | 1 | 1 | Fortune, Miss. Alice Elizabeth | female | 24.0 | 3 | 2 | 19950 | 263.0 | C23 C25 C27 | S |
| 438 | 439 | 0 | 1 | Fortune, Mr. Mark | male | 64.0 | 1 | 4 | 19950 | 263.0 | C23 C25 C27 | S |
ParchとSibSpの数が合わないような気がします。
うまく抽出できていないのでしょうか?
Fortune, Mr. Markが64才でSibSpが1になっています。
同年代の人が抽出されなければ変ですね。
# 他にParchが4の人を表示
df.loc[(df["Parch"] == 4)]| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 167 | 168 | 0 | 3 | Skoog, Mrs. William (Anna Bernhardina Karlsson) | female | 45.0 | 1 | 4 | 347088 | 27.900 | NaN | S |
| 360 | 361 | 0 | 3 | Skoog, Mr. Wilhelm | male | 40.0 | 1 | 4 | 347088 | 27.900 | NaN | S |
| 438 | 439 | 0 | 1 | Fortune, Mr. Mark | male | 64.0 | 1 | 4 | 19950 | 263.000 | C23 C25 C27 | S |
| 567 | 568 | 0 | 3 | Palsson, Mrs. Nils (Alma Cornelia Berglund) | female | 29.0 | 0 | 4 | 349909 | 21.075 | NaN | S |
他にParchが4の人を抽出してみましたが、Fortune家の人はFortune, Mr. Markさんしかいなそうです。他の情報と照らし合わせても別名になっているわけでもなさそうです。
# 名前にFortuneという文字列が含まれる人を表示
df.loc[(df["Name"].str.contains('Fortune'))]| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 27 | 28 | 0 | 1 | Fortune, Mr. Charles Alexander | male | 19.0 | 3 | 2 | 19950 | 263.0 | C23 C25 C27 | S |
| 88 | 89 | 1 | 1 | Fortune, Miss. Mabel Helen | female | 23.0 | 3 | 2 | 19950 | 263.0 | C23 C25 C27 | S |
| 341 | 342 | 1 | 1 | Fortune, Miss. Alice Elizabeth | female | 24.0 | 3 | 2 | 19950 | 263.0 | C23 C25 C27 | S |
| 438 | 439 | 0 | 1 | Fortune, Mr. Mark | male | 64.0 | 1 | 4 | 19950 | 263.0 | C23 C25 C27 | S |
ここまで見てきましたが、全部で6人(両親/子供・兄弟・親戚・自分)のはずですが、やっぱり数が合いません。
ここまできたら、testデータに他のFortune家のメンバーが含まれているのかも知れないので確認してみます。
# テストデータの読み込み
df_test = pd.read_csv("/Users/hinomaruc/Desktop/notebooks/titanic/test.csv")# 名前にFortuneという文字列が含まれる人を表示
df_test.loc[(df_test["Name"].str.contains('Fortune'))]| PassengerId | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 53 | 945 | 1 | Fortune, Miss. Ethel Flora | female | 28.0 | 3 | 2 | 19950 | 263.0 | C23 C25 C27 | S |
| 69 | 961 | 1 | Fortune, Mrs. Mark (Mary McDougald) | female | 60.0 | 1 | 4 | 19950 | 263.0 | C23 C25 C27 | S |
ビンゴです!Fortune, Miss. Ethel FloraさんとFortune, Mrs. Markさんが抽出されました。TicketもFareも同じです。
次は、Fareの263.0という値が合計料金なのか1人当たりの料金なのか検討をつけようと思います。
# PclassごとのFareの中央値を確認
df.groupby(["Pclass"]).median()| PassengerId | Survived | Age | SibSp | Parch | Fare | |
|---|---|---|---|---|---|---|
| Pclass | ||||||
| 1 | 472.0 | 1.0 | 37.0 | 0.0 | 0.0 | 60.2875 |
| 2 | 435.5 | 0.0 | 29.0 | 0.0 | 0.0 | 14.2500 |
| 3 | 432.0 | 0.0 | 24.0 | 0.0 | 0.0 | 8.0500 |
Pclass=1の人物全体の中央値の料金は60.2875のようです。
# PclassごとにSibSpとParchが0の中央値を確認 (一人当たりの料金を確認できる)
df.loc[(df["SibSp"] == 0) & (df["Parch"] == 0)].groupby(["Pclass"]).median()| PassengerId | Survived | Age | SibSp | Parch | Fare | |
|---|---|---|---|---|---|---|
| Pclass | ||||||
| 1 | 494.0 | 1.0 | 38.5 | 0.0 | 0.0 | 31.0000 |
| 2 | 399.5 | 0.0 | 31.0 | 0.0 | 0.0 | 13.0000 |
| 3 | 473.5 | 0.0 | 26.0 | 0.0 | 0.0 | 7.8958 |
Pclass=1の1人当たりの中央値の料金は31のようです。
# PclassごとにSibSpが1とParchが0の中央値を確認 (2人での料金を確認できる)
df.loc[(df["SibSp"] == 1) & (df["Parch"] == 0)].groupby(["Pclass"]).median()| PassengerId | Survived | Age | SibSp | Parch | Fare | |
|---|---|---|---|---|---|---|
| Pclass | ||||||
| 1 | 454.0 | 1.0 | 36.0 | 1.0 | 0.0 | 76.7292 |
| 2 | 384.0 | 0.0 | 29.5 | 1.0 | 0.0 | 26.0000 |
| 3 | 359.5 | 0.0 | 25.0 | 1.0 | 0.0 | 15.0000 |
Pclass=1の2人当たりの料金の中央値は77のようです。
# Fortune家の一人当たりの料金を計算 (263が合算だった場合を仮定)
263.0 / 643.833333333333336
# PclassごとにSibSpとParchが0の平均値を確認 (一人当たりの料金を確認できる)
df.loc[(df["SibSp"] == 0) & (df["Parch"] == 0)].groupby(["Pclass"]).mean()| PassengerId | Survived | Age | SibSp | Parch | Fare | |
|---|---|---|---|---|---|---|
| Pclass | ||||||
| 1 | 478.458716 | 0.532110 | 41.005814 | 0.0 | 0.0 | 63.672514 |
| 2 | 432.086538 | 0.346154 | 33.736559 | 0.0 | 0.0 | 14.066106 |
| 3 | 459.435185 | 0.212963 | 28.235556 | 0.0 | 0.0 | 9.272052 |
Pclass=1の1人当たりの平均運賃は64のようです。
ここまでの結果をまとめ
・Pclass=1の1人当たりの中央値の料金は31
・Pclass=1の2人当たりの中央値の料金は77
・Pclass=1の1人当たりの平均料金は64
・Fortune家のFareは263で、合計値と仮定して一人当たりに換算すると43.8
上記結果から、Fareの値は(Fortune家に限っては)同行家族全員の合算値になっていると考えれます。
ですので、Fareの料金やSibSpの数値が大きいとしても外れ値ではないと判断しました。
2022/04/26追記
Pclass=2とPclass=3の場合も確認すると、同行家族がいてもチケット番号が異なる人と同じ人両方のパターンがありました。
チケット番号が異なる場合は、Fareは合算にはなっていないと思われますのでご認識ください。
2022/04/27追記
Fareについて調べてみました。
Fare turns out to be a really complicated variable. It's based on the price of the ticket sold to a traveling group (often a family). It's not the cost of the ticket for each individual (unless the Fare was for 1 person). So if you sort the table by Ticket, you'll see that people who share the same Ticket had the same Fare. 引用: https://www.kaggle.com/c/titanic/discussion/33087
チケットは家族などのグループ単位で販売されているので、1人でない限りやはり合算値になっているようです。
また、年齢によるディスカウントや関係者など無料で乗船した人のFareは0になっているようです。
そのため1人1人の運賃を正確に計算することは難しいようです。
まとめ
タイタニックのデータセットの外れ値の検出と処理をしてみました。
今回はきれいなデータでしたので処理をするものがありませんでしたが、ウェブデータで何回もPVが飛んできてしまった場合などで極端に数値が多くなる場合があります。その場合は機械学習にかける前に除外や数値を丸めたりする必要がありますので、また他のデータセットの分析をする際に取り組みたいと思います。
参考
・https://ja.wikipedia.org/wiki/外れ値
・https://statisticsbyjim.com/basics/interquartile-range/
・https://statisticsbyjim.com/basics/outliers/
・https://www.statisticshowto.com/grubbs-test/
・https://www.degruyter.com/document/doi/10.1515/dema-2021-0041/html
・https://stats.stackexchange.com/questions/355943/how-to-estimate-the-scale-factor-for-mad-for-a-non-normal-distribution
・https://www.statology.org/modified-z-score/