前回ニューラルネットワークの概念についてまとめました。
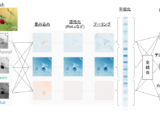
しばらく勉強していたのもあって時間がかかってしまいましたが、今回はPythonで多層パーセプトロン(Multi-Layer Perceptron)の実装をしてみたいと思います。
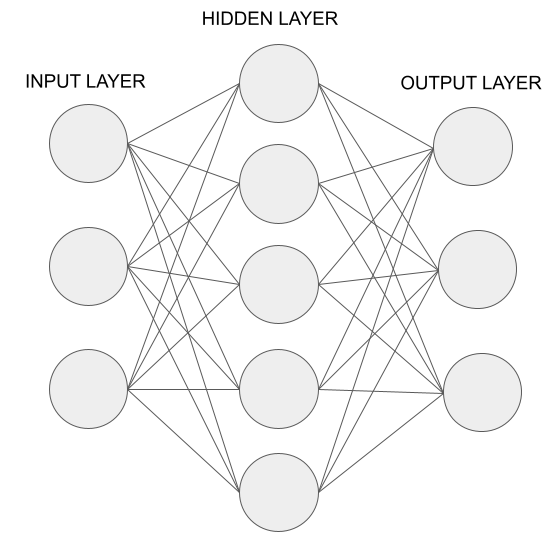
まず、前回の記事のおさらいになってしまいますが、(人工)ニューラルネットワークは私たちの脳内の神経細胞のネットワークを模倣したものになっています。
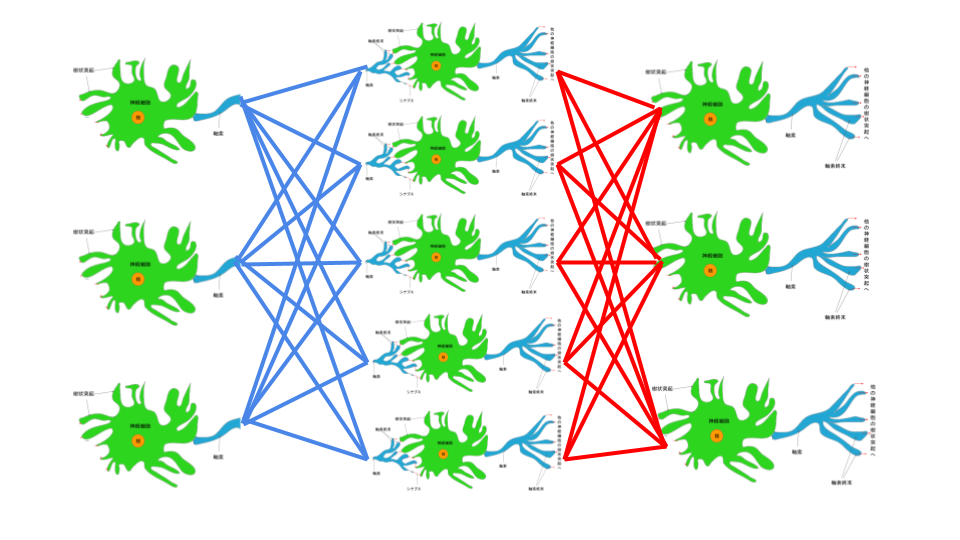
私たちの脳内の神経細胞のネットワークとは下記のように、ニューロンという単位の集まりで「樹状突起」、「軸索」、「軸索終末」、「シナプス」といった機能で構成されています。
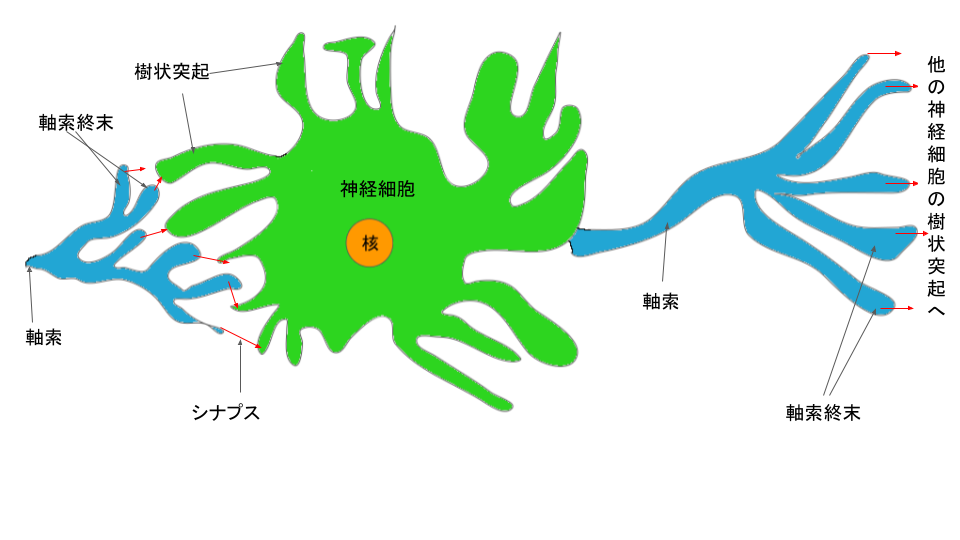
そして、すべてのニューロンは電気信号を軸索に沿って樹状突起から他方の軸索終末へと伝達することによって、私たちは光、音、圧力、熱などを感知しています。(参考: ニューラルネットワーク自作入門 p48)
下記は3層の多層パーセプトロンの図を脳内の神経細胞に置き換えたらこうなるであろうというのを図にしたものです。
樹状突起へと伝達される情報をインプットととして、軸索・軸索終末を通って他のニューロンの樹状突起へと連なっています。
それではイメージを掴んだところで、多層パーセプトロンの実装をしていきたいと思います。
(オプション) 行列計算の確認
多層パーセプトロンの実装で重要なのが、行列積の計算です。
行列積を計算することによってニューラルネットワークのノード間の重みを低コストで更新することが可能になります。
numpyのdotメソッドで実現が可能です。
import numpy as np
import scipy.special
np.dot(np.array([[1,2],[3,4]]),np.array([[5,6],[7,8]]))
array([[19, 22],
[43, 50]])
計算方法と結果は素直に行列積計算サイトを参照しました 笑
c11 = 1 x 5 + 2 x 7 = 19
c12 = 1 x 6 + 2 x 8 = 22
c21 = 3 x 5 + 4 x 7 = 43
c22 = 3 x 6 + 4 x 8 = 50
参考: https://matrix.reshish.com/multCalculation.php
順方向伝搬 (Forward propagation)
まずは下記のようなシンプルな多層パーセプトロンを実装してみようと思います。
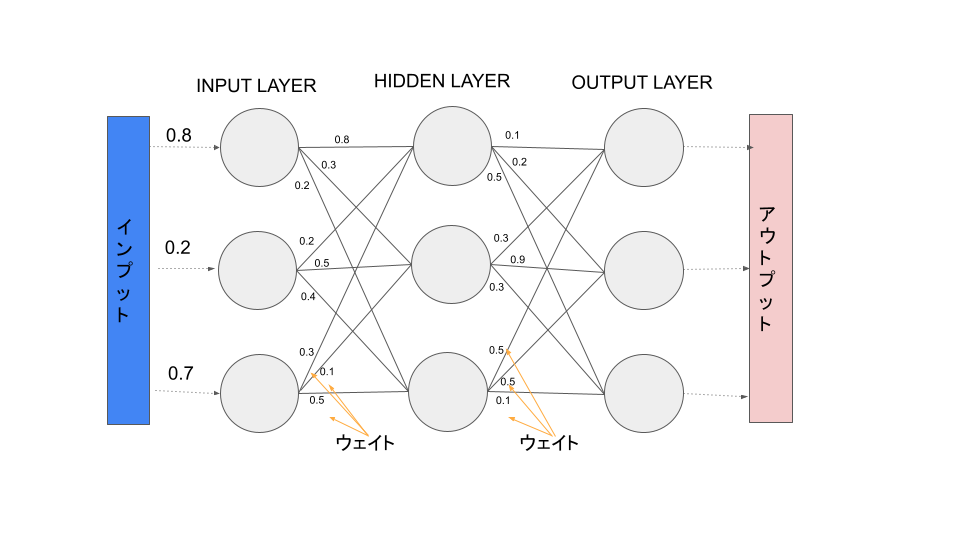
インプットとして[0.8,0.2.0.7]という数値を与えた時に、設定したウェイトによって情報を隠れ層に伝達し何かしらのアウトプットを出力するニューラルネットワークを構築します。
ウェイトの値は自分で決めたランダムな値を割り当てています。(初期値の設定方法は他にも正規分布に従った乱数を使う方法などがあるようです)
順方向伝搬とは、ニューラルネットワークでインプットデータが前方へとアウトプット作成するために流れていく過程のことになります。データは隠れ層によって処理され活性化関数の適用を経てアウトプットレイヤーの方向へと流れていきます、
As the name suggests, the input data is fed in the forward direction through the network. Each hidden layer accepts the input data, processes it as per the activation function and passes to the successive layer.
引用: https://towardsdatascience.com/forward-propagation-in-neural-networks-simplified-math-and-code-version-bbcfef6f9250
Forward propagation is where input data is fed through a network, in a forward direction, to generate an output. The data is accepted by hidden layers and processed, as per the activation function, and moves to the successive layer. The forward flow of data is designed to avoid data moving in a circular motion, which does not generate an output.
引用: https://h2o.ai/wiki/forward-propagation/
活性化関数を利用する理由としては出力を自然界で見られる信号の応答にするため (引用: ニューラルネットワーク自作入門 p75) で、適用することによりモデルに非線形性を与えより柔軟な表現力を持たせることが出来るようです。
活性化関数として利用するものは色々考えられており、Sigmoid、tanh、ReLU関数などが存在します。この中でも最近はReLUが他の活性化関数よりも計算が容易で、勾配消失問題が低減されるなどといった理由から使われることが多いようです。
勾配消失問題については「勾配消失問題とは?」が数式を含めて詳しく説明をされていました。
順方向伝搬の実装
それではPythonで実装していきたいと思います。ニューラルネットワーク自作入門という本を参考にしています。
単純な3層の多層ニューラルネットワークですし、活性化関数は本に習ってシグモイド関数を利用します。
ReLUを使っても良いかもしれませんが、ReLUを活性化関数として使用する場合は、その特性からかアウトプットレイヤーやRNNでは通常使わない方がいいようです。詳細は下記引用先の記事をご確認ください。
The ReLU function is the default activation function for hidden layers in modern MLP and CNN neural network models.
We do not usually use the ReLU function in the hidden layers of RNN models. Instead, we use the sigmoid or tanh function there.
We never use the ReLU function in the output layer.
引用: https://towardsdatascience.com/how-to-choose-the-right-activation-function-for-neural-networks-3941ff0e6f9c
インプットと初期の重み行列を準備
import numpy as np
import scipy
# インプットリスト
I = np.array([0.8,0.2,0.7])
Iarray([0.8, 0.2, 0.7])
# 重み(第一層から第二層)
wih = np.array([[0.8, 0.2, 0.3],
[0.3, 0.5, 0.1],
[0.2, 0.4, 0.5]])
wih
array([[0.8, 0.2, 0.3],
[0.3, 0.5, 0.1],
[0.2, 0.4, 0.5]])
# 重み(第二層から第三層)
who = np.array([[0.1, 0.3, 0.5],
[0.2, 0.9, 0.5],
[0.5, 0.3, 0.1]])
who
array([[0.1, 0.3, 0.5],
[0.2, 0.9, 0.5],
[0.5, 0.3, 0.1]])
準備が整いました。入力値と重みを使い次の層に情報を伝達させていきましょう。
まずは、入力層から隠れ層への情報伝達です。
入力層から隠れ層への情報伝達
入力層では単にインプットを表すだけ (引用:ニューラルネットワーク自作入門 p72)なので、活性化関数を適用する必要はないようです。
そのため、単純にI = [0.8,0.2,0.7]の値をそのまま隠れ層へ重みを考慮して伝達させてあげれば良いようです。
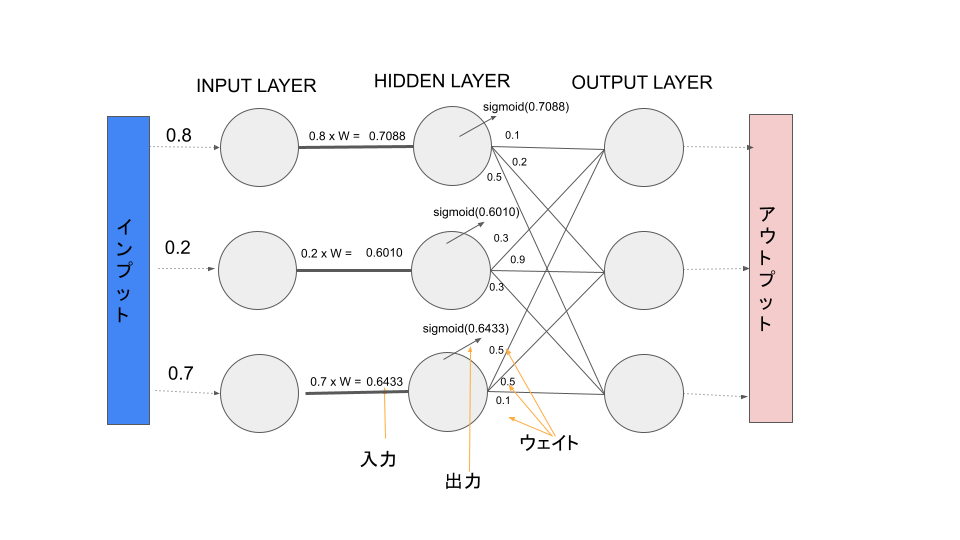
入力層の各ノードの値とノード間の重みで次の層のインプットとなる値を計算します。
# 順番が逆だと異なるアウトプットになるので注意。np.dot(I,wih)はダメ
hidden_layer_input = np.dot(wih,I)
hidden_layer_inputarray([0.89, 0.41, 0.59])
入力層 → 隠れ層へと伝達される数値が計算出来ました。
次に入力層から伝達されてきた値を隠れ層のノードにて活性化関数を適用してあげることにより、次に伝達する値を出力します。
# シグモイド関数を適用
hidden_layer_output_sig = scipy.special.expit(hidden_layer_input)
hidden_layer_output_sigarray([0.70889017, 0.60108788, 0.64336515])
計算できました。この値を次の出力層へと伝達します。
print('sigmoid(1) ->',scipy.special.expit(1))
print('sigmoid(2) ->',scipy.special.expit(2))
print('sigmoid(100) ->',scipy.special.expit(100))
print('sigmoid(-1) ->',scipy.special.expit(-1))
print('sigmoid(-2) ->',scipy.special.expit(-2))
print('sigmoid(-100) ->',scipy.special.expit(-100))
print('sigmoid(0) ->',scipy.special.expit(0))sigmoid(1) -> 0.7310585786300049 sigmoid(2) -> 0.8807970779778823 sigmoid(100) -> 1.0 sigmoid(-1) -> 0.2689414213699951 sigmoid(-2) -> 0.11920292202211755 sigmoid(-100) -> 3.7200759760208356e-44 sigmoid(0) -> 0.5
隠れ層から出力層への情報伝達
入力層から伝達されてきた値を隠れ層で受け取り、さらに次の出力層へと伝達します。
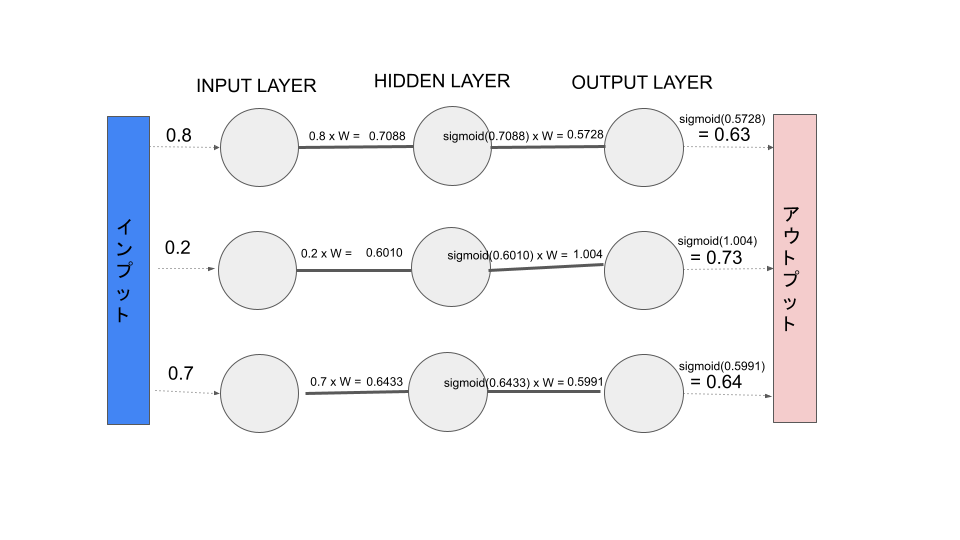
final_layer_input = np.dot(who,hidden_layer_output_sig)
final_layer_inputarray([0.57289795, 1.0044397 , 0.59910796])
隠れ層 → 出力層へと伝達される数値が計算出来ました。
次に隠れ層から伝達されてきた値を出力層のノードにて活性化関数を適用してあげてアウトプットの値を出力します。
final_layer_output_sig = scipy.special.expit(final_layer_input)
final_layer_output_sigarray([0.63943159, 0.73193058, 0.6454522])
結果が出てきました。最終的に順方向伝搬によって、インプットとして[0.8,0.2.0.7]という数値を与えた時に、アウトプットとして[0.63943159, 0.73193058, 0.6454522]という値が出力されました。
ちなみに当然ですが、ウェイトの値が変わると結果も変わります。
import numpy as np
import scipy
# インプットリスト
I = np.array([0.8,0.2,0.7])
# 重み(第一層から第二層)
wih = np.array([[0.8, 0.2, 0.3],
[0.3, 0.5, 0.1],
[0.2, 0.4, 0.5]])
# 重み(第二層から第三層)
who = np.array([[0.1, 0.3, 0.5],
[0.2, 0.9, 0.5],
[0.5, 0.3, 0.1]])
hidden_layer_input = np.dot(wih,I)
# シグモイド関数を適用
hidden_layer_output_sig = scipy.special.expit(hidden_layer_input)
final_layer_input = np.dot(who,hidden_layer_output_sig)
final_layer_output_sig = scipy.special.expit(final_layer_input)final_layer_output_sigarray([0.63943159, 0.73193058, 0.6454522 ])誤差逆伝播法 (Back propagation)
順方向伝搬はどちらかといえば分かりやすかったですが、誤差逆伝搬法は難しいですね。調べてみてもどうも自分の中で納得感が湧いてくるまで時間がかかっているという感じです。
これまでで理解していることと言ったら、出力したアウトプットと求めているアウトプット(期待値)との差(エラー)を計算して、それぞれの重みの比重により各ノードのエラー具合を計算して重みを全体的に良い方向になるように更新していくというような感じです。
他の本も読んで、もう少し絵にしたり数式も含めてきちんと理解を進めていきたいと思います。
とりあえず上記で言語化したプロセスを、ニューラルネットワーク自作入門を参考にしながらPythonでやってみます。
誤差逆伝播法の実装
# 正解データを準備
targets = np.array([0.5,0.99,0.6])
targetsarray([0.5 , 0.99, 0.6 ])
出力は活性化関数で表現できる範囲内で設定しないと、「飽和」という現象を引き起こしより良い重みを学習する能力が低下するようです。
そのためシグモイド関数の幅である0~1の間で設定しました。
output_errors = targets - final_layer_output_sig
output_errorsarray([-0.13943159, 0.25806942, -0.0454522])
# 出力誤差と隠れ層と出力層の間の重みの比重から隠れ層の誤差を算出
hidden_errors = np.dot(who.T, output_errors)
hidden_errorsarray([0.01494463, 0.17679734, 0.05477369])
# 隠れ層と出力層の間の重みの更新。学習率を設定し一気に更新しすぎないようにしている。(最適な値を飛び越えてしまうのを緩和する)
learning_rate = 0.1
who += learning_rate * np.dot((output_errors * final_layer_output_sig * (1.0 - final_layer_output_sig)), np.transpose(hidden_layer_output_sig))
who
array([[0.10009555, 0.30009555, 0.50009555],
[0.20009555, 0.90009555, 0.50009555],
[0.50009555, 0.30009555, 0.10009555]])
# 入力層と隠れ層の間の重みの更新。ここでも学習率を設定している。
wih += learning_rate * np.dot((hidden_errors * hidden_layer_output_sig * (1.0 - hidden_layer_output_sig)), np.transpose(I))
wih
array([[0.80197431, 0.20197431, 0.30197431],
[0.30197431, 0.50197431, 0.10197431],
[0.20197431, 0.40197431, 0.50197431]])
新しい重みを求めることが出来ました。更新した重みでもう一度順方向伝搬を実行してみます。
# もう一回
hidden_layer_input = np.dot(wih,I)
print(hidden_layer_input)
print("---")
hidden_layer_output_sig = scipy.special.expit(hidden_layer_input)
print(hidden_layer_output_sig)
print("---")
final_layer_input = np.dot(who,hidden_layer_output_sig)
print("final_layer_input",final_layer_input)
print("---")
final_layer_output_sig = scipy.special.expit(final_layer_input)
print("final_layer_output_sig",final_layer_output_sig)[0.89335633 0.41335633 0.59335633] --- [0.70958232 0.60189239 0.64413487] --- final_layer_input [0.57378025 1.00587392 0.59995923] --- final_layer_output_sig [0.63963499 0.73221189 0.64564698]
アウトプットが[0.63943159, 0.73193058, 0.6454522]から[0.63963499 0.73221189 0.64564698]に変わりました。
正解データは[0.5,0.99,0.6]です。
正解データの0.99に引っ張られているのでしょうか?すべての値が若干増えたようです。
あとはこの作業を何回も繰り返してベストな重みを求めていくことになります。
まとめ
Pythonで多層パーセプトロンを実装することが出来ました。
いままでSklearnで1行で実行できていたので自分で実装するとこんなに大変な作業だったとは実感が湧きませんでした。(本を参考にしているだけですが 笑)
ただ使うだけではなく、こうして各アルゴリズムを自分で実装することで理解を深めていきたいなと考えています。