今日、IoTデバイスの普及により膨大なセンサーデータが取得されるようになりました。
今までセンサーデータを扱う機会はあまりなかったのですが、これからどんどん活用するようになるはずなので先にデータ加工方法だけでもと思いコードを作成してみました。
基本的にセンサーデータは通常短い間隔で取得される時系列の波形データと同じようなものだという印象を持ちました。
とりあえずスマホでも取得しやすそうな加速度センサーを分析するという仮定で色々調べています。
加速度センサーのデータ加工について
加速度センサーについてはYahoo! JAPAN Tech Blogの「スマホの加速度センサーから車の運転特性を求める 〜 Yahoo!カーナビの挑戦」という記事が参考になりました。
とりあえず今回サンプルとして使うデータは加速度(x軸)、加速度(y軸)、加速度(z軸)、速度の4変数を取得しているということにしようと思います。
特徴量としては使えるかは分かりませんが、下記変数を追加で作成しました。
・乗数加速度
・フーリエ変換
・ウェーブレット変換
・短時間フーリエ変換
最終的に機械学習に投入出来るデータにしようと思っていますが、目的によって加工方法が変わると思っています。
例えば下記のような分析がセンサーデータで可能かなと思います。
- 次の数秒を予測 → 時系列分析
- 特異点抽出 → 異常値検知
- 波形からアクティビティを検知 → パターンマッチング?
今回加工するのは3番を想定しました。
例えばある期間(数秒)の波形データからアクティビティ(歩行、走る、座るなど)を検知するようなテーマを勝手に設定しています。
そのため、歩行や着席時の波形データをいくつも集めて、それぞれの波形データを1行のデータに集約し、機械学習に投入することで分類問題を解けるようにしようと思います。
あくまで机上の空論なので自分のスマホでデータを集めて分類してみるなどはやってみたいと思います 笑
それでは加工していきます。1行に集約するのは処理の一番最後なので集約していないデータを分析に使う何てことも出来ると思います。
venv環境の作成
python3.8 -m venv venv-sensor
source venv-sensor/bin/activate
(venv-sensor) pip install pip -U
(venv-sensor) pip install wheel
(venv-sensor) pip install ipykernel
(venv-sensor) pip install PyWavelets
(venv-sensor) pip install pandas
(venv-sensor) pip install scikit-learn
(venv-sensor) pip install matplotlib
(venv-sensor) pip install seaborn
(venv-sensor) python3 -m ipykernel install --user --name venv-sensor --display-name "venv-sensor"データの読み込み または 生成
データがあればcsvなどのデータの読み込み、なければシュミレーションとしてデータの生成を行ってみたいと思います。
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
import pywt
import os
from scipy import signal
from itertools import combinations as comb# 描画設定
from IPython.display import HTML
import seaborn as sns
from matplotlib import ticker
import matplotlib.pyplot as plt
sns.set_style("whitegrid")
from matplotlib import rcParams
rcParams['font.family'] = 'Hiragino Sans' # Macの場合
#rcParams['font.family'] = 'Meiryo' # Windowsの場合
#rcParams['font.family'] = 'VL PGothic' # Linuxの場合
rcParams['xtick.labelsize'] = 12 # x軸のラベルのフォントサイズ
rcParams['ytick.labelsize'] = 12 # y軸のラベルのフォントサイズ
rcParams['axes.labelsize'] = 18 # ラベルのフォントとサイズ
rcParams['figure.figsize'] = 18,8 # 画像サイズの変更(inch)csvデータの読み込み
# センサーデータのCSVがある場合は下記で読み込む
#BASE_DIR="/Users/hinomaruc/Desktop/blog/dataset/sensor/"
#df = pd.read_csv(os.path.join(BASE_DIR,"sensor.csv"),header=None,names=["gx","gy","gz","velocity"])データの生成
# データ数 (0.01秒間隔の合計1秒のデータと仮定)
num_points = 100
# ランダムで-3Gから3Gのデータを作成する
gx = np.random.uniform(-3, 3, num_points)
gy = np.random.uniform(-3, 3, num_points)
gz = np.random.uniform(-3, 3, num_points)
# 速度は0から120kmまでの間でランダム
velocity = np.random.uniform(0, 120, num_points)
# センサーデータを模倣したデータフレームの作成
df = pd.DataFrame({
'gx': gx,
'gy': gy,
'gz': gz,
'velocity': velocity
})
# 上から5件を確認
print(df.head())
# 描画
df[["gx","gy","gz","velocity"]].plot(secondary_y=["velocity"],legend=True)
gx gy gz velocity
0 -2.261571 2.914784 0.283359 29.453788
1 -2.640064 -1.774366 1.282123 20.977121
2 -0.594036 -2.727081 -2.298931 23.397042
3 -1.278850 1.812851 -0.789989 41.808104
4 0.193807 2.330460 2.133371 97.940225

ものすごく激しく動いているようなデータになりました。速度の間隔はもう少し狭めても良かったかも知れません (短時間で急激に変わりすぎ 笑)
特徴量エンジニアリング
乗数加速度、フーリエ変換、ウェーブレット変換、短時間フーリエ変換をセンサーデータの特徴量として作成しようと思います。
乗数加速度
乗法加速度(multiplicative acceleration)は、加速度センサーデータを分析するための特徴量エンジニアリングの1つで、加速度センサーから得られた信号の大きさを表す指標です。加速度センサーは、3つの軸(X、Y、Z)に沿って物体の加速度を測定します。乗法加速度は、3つの軸の加速度の絶対値を掛け合わせたもので、以下の式で表されます。
乗法加速度 = √(gx^2 gy^2 gz^2)
ここで、gx、gy、gzはそれぞれX、Y、Z軸方向の加速度を表します。(デバイスの置き方などでどの軸がどちらを向いているかは変わると思います)
乗法加速度は、加速度の大きさが均等に分散されている場合に最大値をとります。これは物体が全方向に均等に加速されている場合に最も高い値を示し、一方向にのみ加速されている場合には低い値を示します。
乗法加速度は、物体の動きの速さや方向を示す指標として使用されます。例えば、スマートフォンのセンサーから乗法加速度を取得することで、歩行やランニングなどの活動の種類や強度、速度、方向などを判別することができます。また、スポーツや健康管理、自動車やドローンの運転制御などの分野でも乗法加速度は重要な特徴量として使用されます。
# 乗数加速度の作成
df['magnitude'] = np.sqrt(df['gx']**2 + df['gy']**2 + df['gz']**2)
# 描画
df[["gx","gy","gz","velocity","magnitude"]].plot(secondary_y=["velocity"],legend=True)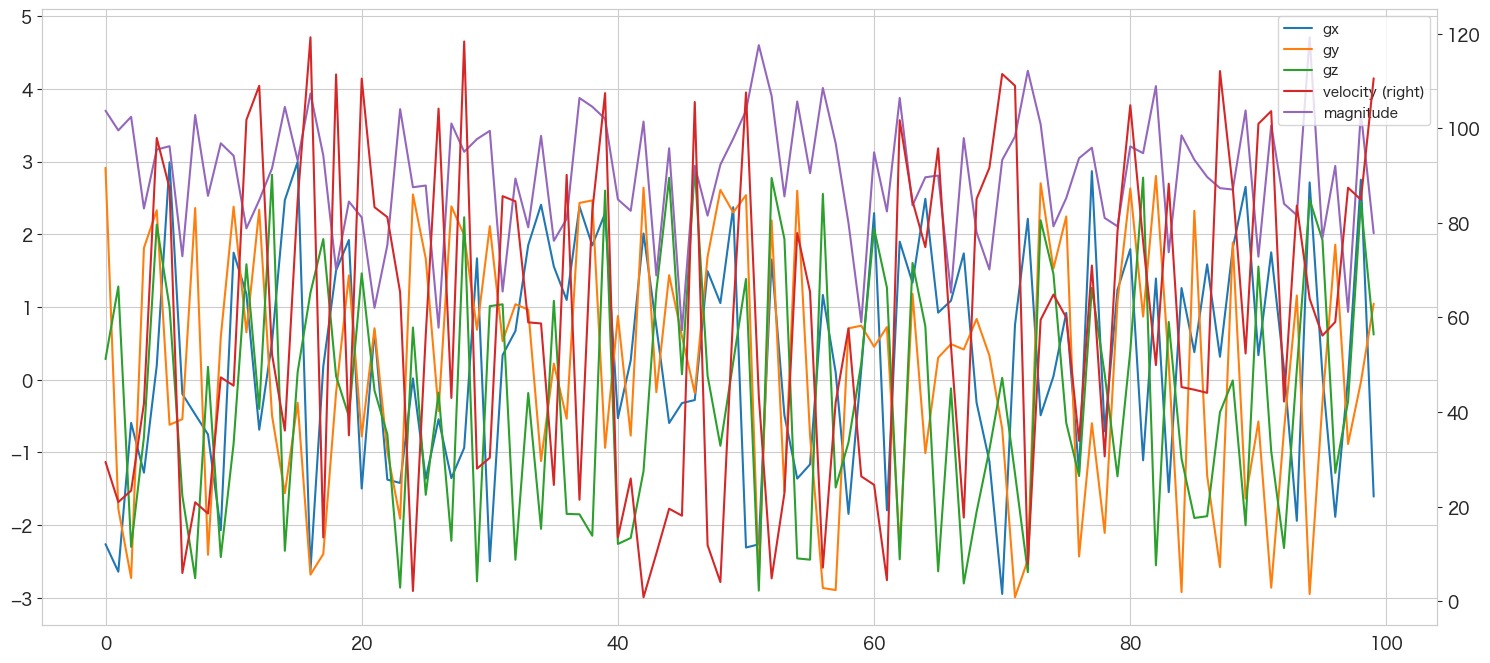
見にくいですが、紫のラインが乗数加速度になります。
フーリエ変換
フーリエ変換(Fourier transform)は、加速度センサーのデータを分析するための特徴量エンジニアリングの1つで、時系列データから周波数成分を抽出する手法です。加速度センサーは、加速度の変化を時系列データとして記録するため、フーリエ変換は特定の周波数領域の情報を抽出するのに適しています。
周波数とは、周期的な現象が繰り返される速さを表す量であり、電気信号や音波、光波などの振動現象を表すためにも使用されます。周波数が高い信号は、短い周期で振動するため、振動数が多くなります。一方、周波数が低い信号は、長い周期で振動するため、振動数が少なくなります。
フーリエ変換は、時間領域の信号を周波数領域の信号に変換することで、信号の周波数成分を解析する手法です。これにより加速度センサーのデータから加速度の周波数スペクトルを解析することができます。
フーリエ変換は、周期的な振動をしている信号に対して有効であり、加速度データに周期的なパターンがある場合に特に有用です。例えば、人の歩行の場合、足の運動は一定の周期性を持ち、フーリエ変換を用いることで、その周期性や振幅を解析することができます。また、振動や振動の周期が不規則な場合にも、フーリエ変換を使用して周波数成分を解析することができます。
下記の例では、データを0.01秒間隔で取得しており、サンプリングレートは100Hzであることが前提となっています。また、周波数軸を設定するために、np.fft.fftfreq関数を使用しています。
ちなみに、サンプリングレート(Sampling rate)が100Hzということは、1秒間に100回のサンプリングが行われることを意味します。つまり、データ収集装置が1秒あたり100回の信号をサンプリングしていることを示しています。
データ収集装置は、加速度センサーから取得した信号をデジタル信号に変換し、ある一定の時間間隔ごとにデータを取得します。この時間間隔をサンプリング間隔(Sampling interval)またはサンプリング期間(Sampling period)と呼び、サンプリングレートはその逆数になります。
例えば、100Hzの場合は、1秒間に100回のサンプリングが行われるため、1回のサンプリング間隔は、1/100秒(0.01秒)となります。
サンプリングレートは、データ収集装置の性能によって異なります。一般的にサンプリングレートが高いほど、収集されるデータはより詳細で正確なものとなりますが、データ量が増加し、処理に必要なリソースが増加するためデータ収集や解析には適切なサンプリングレートを選択する必要があります。
# フーリエ変換
freqs = np.fft.fftfreq(len(df), 0.01) # 周波数軸
df["fft_gx"] = np.abs(np.fft.fft(df.gx))
df["fft_gy"] = np.abs(np.fft.fft(df.gy))
df["fft_gz"] = np.abs(np.fft.fft(df.gz))
df["fft_mag"] = np.abs(np.fft.fft(df.magnitude))
# プロット
df[["fft_gx","fft_gy","fft_gz","fft_mag"]].plot()
plt.show()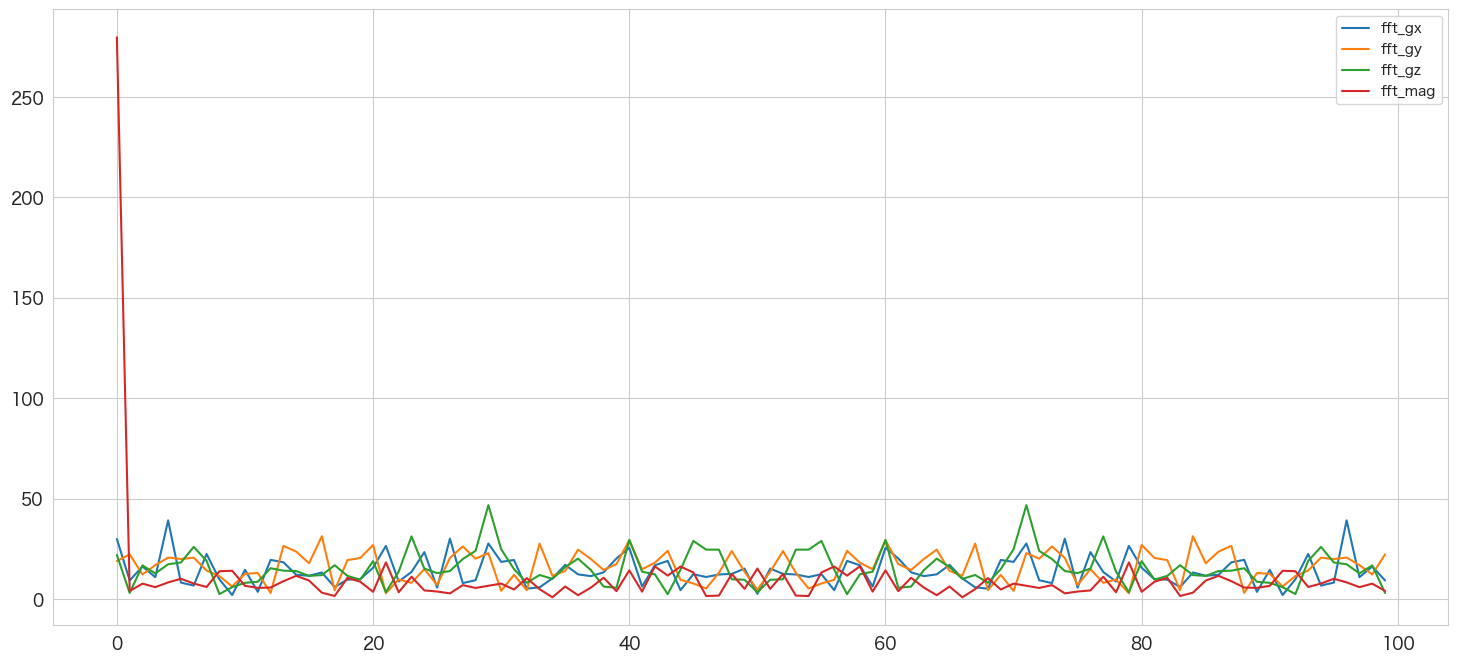
ウェーブレット変換
ウェーブレット変換(Wavelet Transform)は、信号解析や画像処理などの分野で広く用いられる信号解析手法の一つです。加速度センサーの分析にも利用されることがあります。
ウェーブレット変換は、信号を時間と周波数の両方の観点から解析することができます。フーリエ変換は周波数の分解能が高い一方で、時間の分解能が低いため、時間と周波数の両方の情報を取得するには限界があります。一方、ウェーブレット変換は、信号を時間と周波数の両方の観点から解析することができ、時間的に局所的な特徴を抽出することが可能です。
ウェーブレット変換では、信号を小波(ウェーブレット)と呼ばれる基底関数で表現します。小波は、周波数が高い場合には短い周期で振動し、周波数が低い場合には長い周期で振動するため、信号の時間と周波数の情報を同時に取得することができます。
# 各軸と乗数加速度をウェーブレット変換する
(cA, cD) = pywt.dwt(df['gx'], 'db1')
df["wvlt_gx"] = np.concatenate([cA,cD])
(cA, cD) = pywt.dwt(df['gy'], 'db1')
df["wvlt_gy"] = np.concatenate([cA,cD])
(cA, cD) = pywt.dwt(df['gz'], 'db1')
df["wvlt_gz"] = np.concatenate([cA,cD])
(cA, cD) = pywt.dwt(df['magnitude'], 'db1')
df["wvlt_mag"] = np.concatenate([cA,cD])
# 描画
df[["wvlt_gx","wvlt_gy","wvlt_gz","wvlt_mag"]].plot()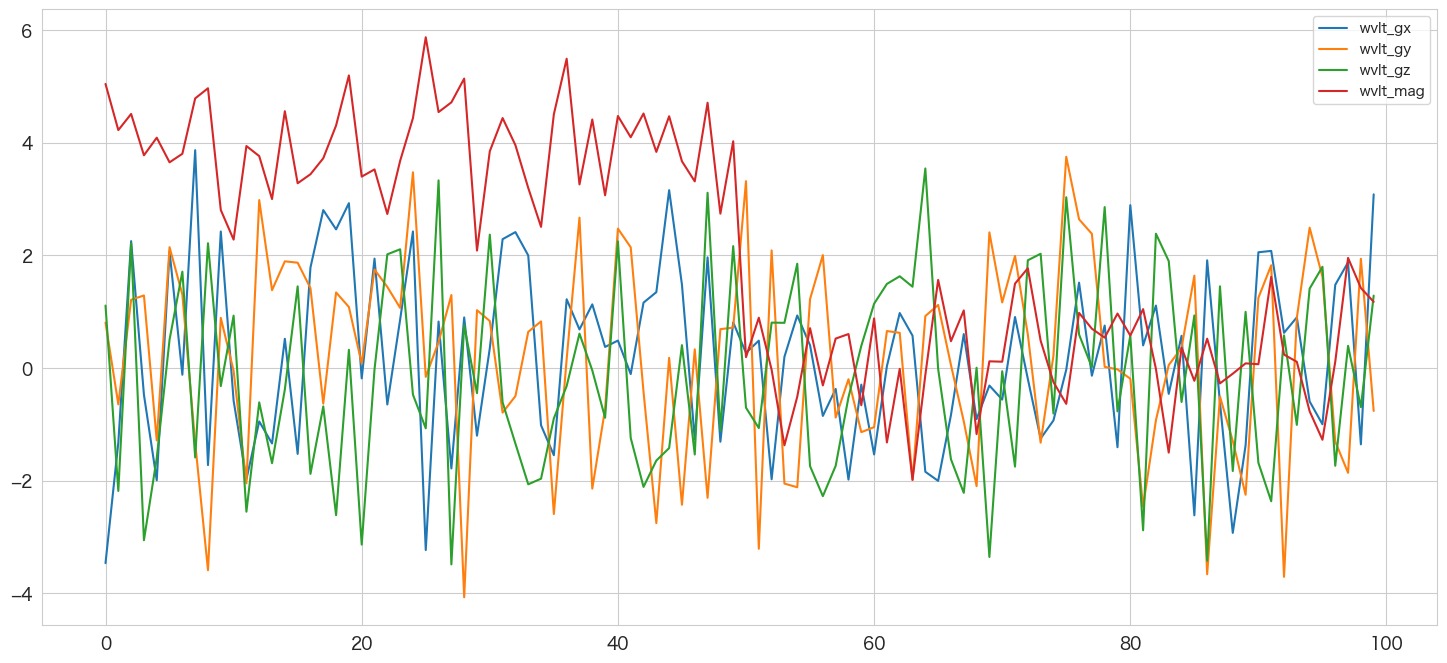
一旦ここまで作成したデータの確認
df.describe()
gx gy gz velocity magnitude fft_gx fft_gy fft_gz fft_mag wvlt_gx wvlt_gy wvlt_gz wvlt_mag count 100.000000 100.000000 100.000000 100.000000 100.000000 100.000000 100.000000 100.000000 100.000000 100.000000 100.000000 100.000000 100.000000 mean 0.298276 0.188684 -0.218661 59.227613 2.796235 13.872922 15.881205 15.094480 10.262078 0.193014 0.165612 -0.131393 2.084202 std 1.561897 1.755063 1.720685 34.561174 0.869905 7.650936 7.540578 8.411919 27.551599 1.578530 1.757413 1.729628 2.065640 min -2.945917 -2.992195 -2.900730 0.848707 0.681543 1.948077 2.840877 2.371833 0.824592 -3.465980 -4.071323 -3.487720 -1.985965 25% -0.980282 -0.948815 -1.846812 27.638811 2.230787 9.077306 10.966856 9.745505 3.988405 -1.004589 -0.973958 -1.604753 0.172799 50% 0.291049 0.434834 -0.163290 58.849328 2.941106 12.230806 14.842993 13.885868 6.542159 0.308863 0.407754 -0.321671 2.018138 75% 1.657064 1.721780 1.231358 87.353054 3.424994 18.299430 20.610452 18.838024 10.572999 1.250834 1.350356 1.314556 3.943310 max 2.996445 2.914784 2.922712 119.230875 4.709752 39.127469 31.222035 46.705548 279.623546 3.865628 3.748534 3.541095 5.869938
短時間フーリエ変換 (STFT)
STFTは、時間領域の局所的な特徴を捉えることができるため、時間分解能が高く、時間的な変化が激しい信号に適しています。
NumPyのnp.fft.fft()関数とSciPyのsignal.stft()関数は、どちらも信号の周波数解析を行うための関数ですが、使用方法や出力結果が異なります。
np.fft.fft()関数は、与えられた時系列データに対して、一度にフーリエ変換を適用して周波数領域のデータを得ます。これにより、時系列データ全体の周波数成分が分かりますが、時間軸に関する情報は失われます。また、np.fft.fft()関数は、フーリエ変換を高速に実行するアルゴリズムであるFFT(高速フーリエ変換)を使用するため、処理速度が非常に速く、簡単に使える点が特徴です。
一方、signal.stft()関数は、ショートタイムフーリエ変換(STFT)を実行します。STFTは、時系列データを複数の短い時間区間(フレーム)に分割し、各フレームごとにフーリエ変換を行うことで、時間軸と周波数軸の両方の情報を取得することができます。これにより、信号の時間変化に対する周波数成分の変化を捉えることができます。また、signal.stft()関数は、フレームサイズやフレームシフトなど、STFTのパラメータを自由に設定できるため、信号の解析に合わせて柔軟に設定することができます。
つまり、np.fft.fft()関数は時間軸の情報を失う代わりに処理速度が速く、signal.stft()関数は時間軸と周波数軸の両方の情報を取得することができますが、より複雑でパラメータの設定が必要です。どちらの関数を使用するかは、解析の目的や要件によって異なるようです。
# サンプリング周波数 (データの取得間隔で決める。)
fs = 100 # 0.01秒ずつと仮定
# 時間の区分。とりあえず四等分を仮定。
nperseg = len(df) // 4
noverlap = nperseg // 5
# 結果格納用
stft_result_dict={}
# 解析対象のカラム
cols = ['gx', 'gy', 'gz','magnitude']
for col in cols:
# 加速度データのショートタイムフーリエ変換
f, t, Zxx = signal.stft(df[col], fs=fs, nperseg=nperseg, noverlap=noverlap)
stft_result_dict["stft_"+col] = np.abs(Zxx)
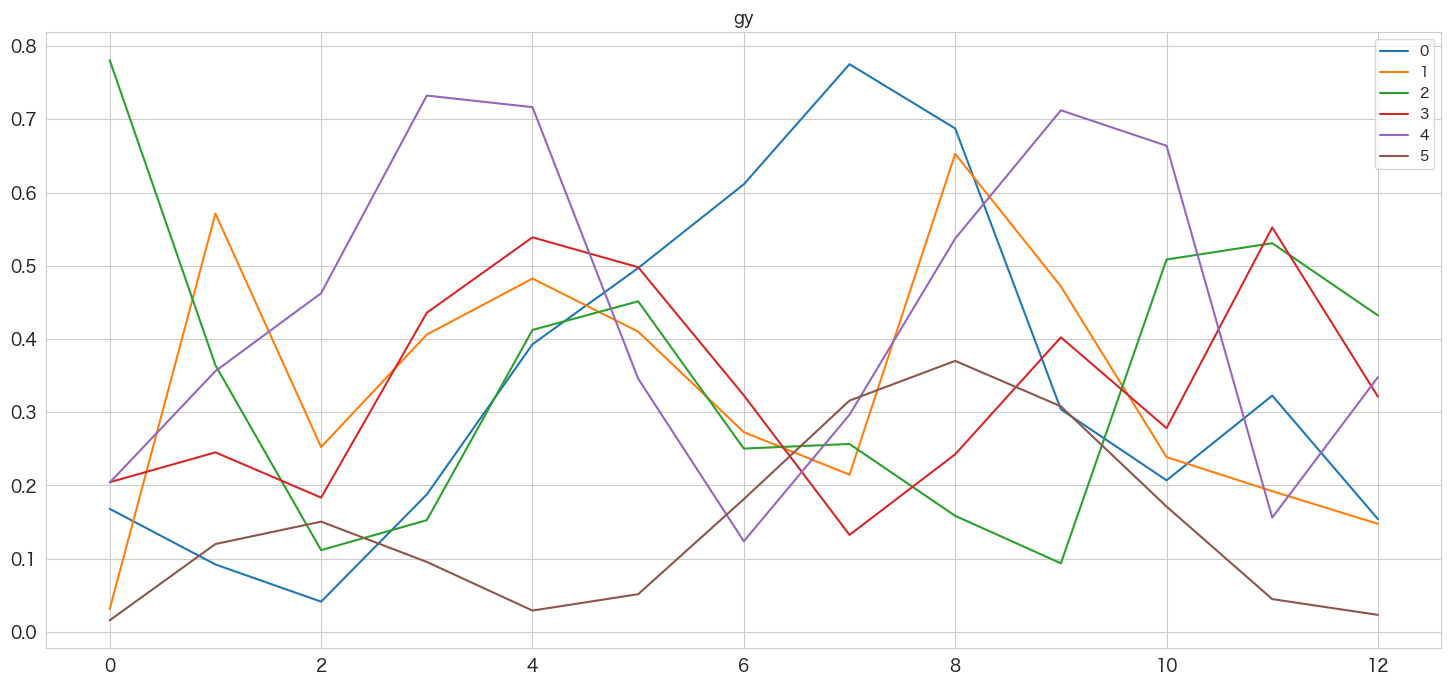
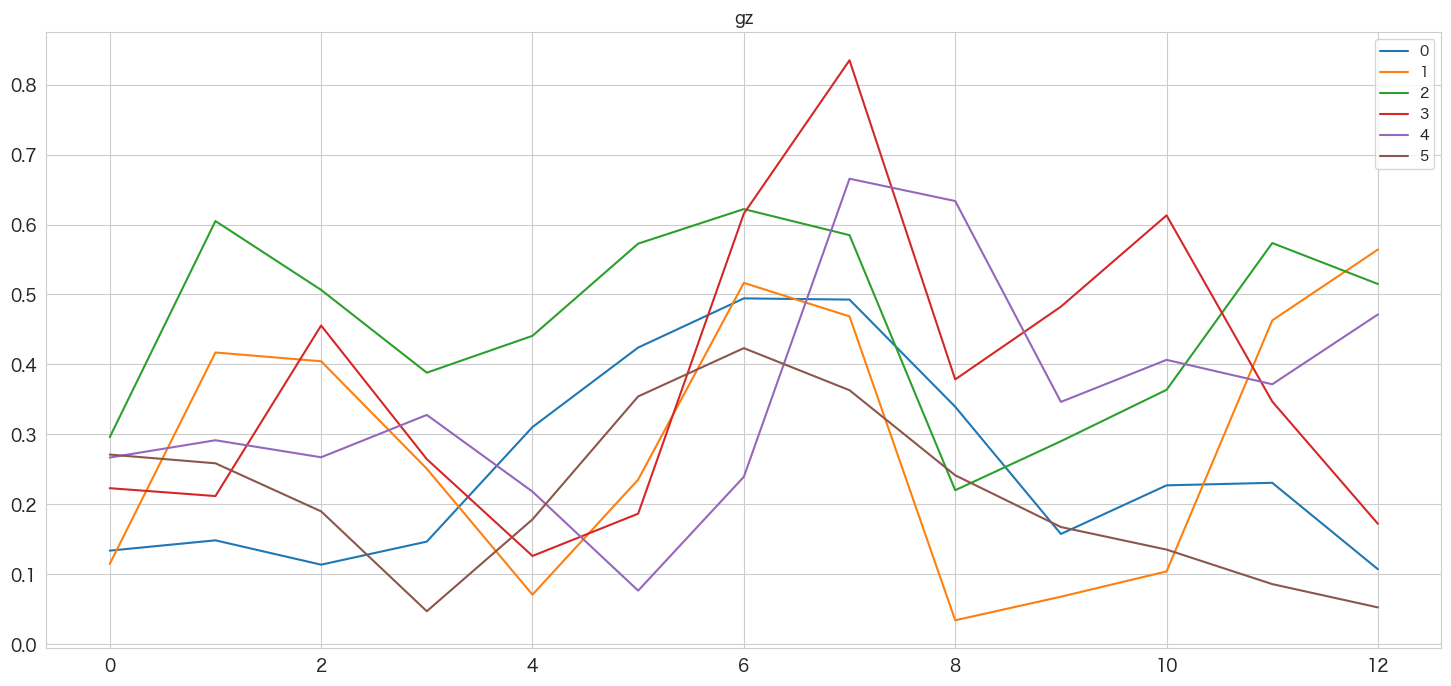
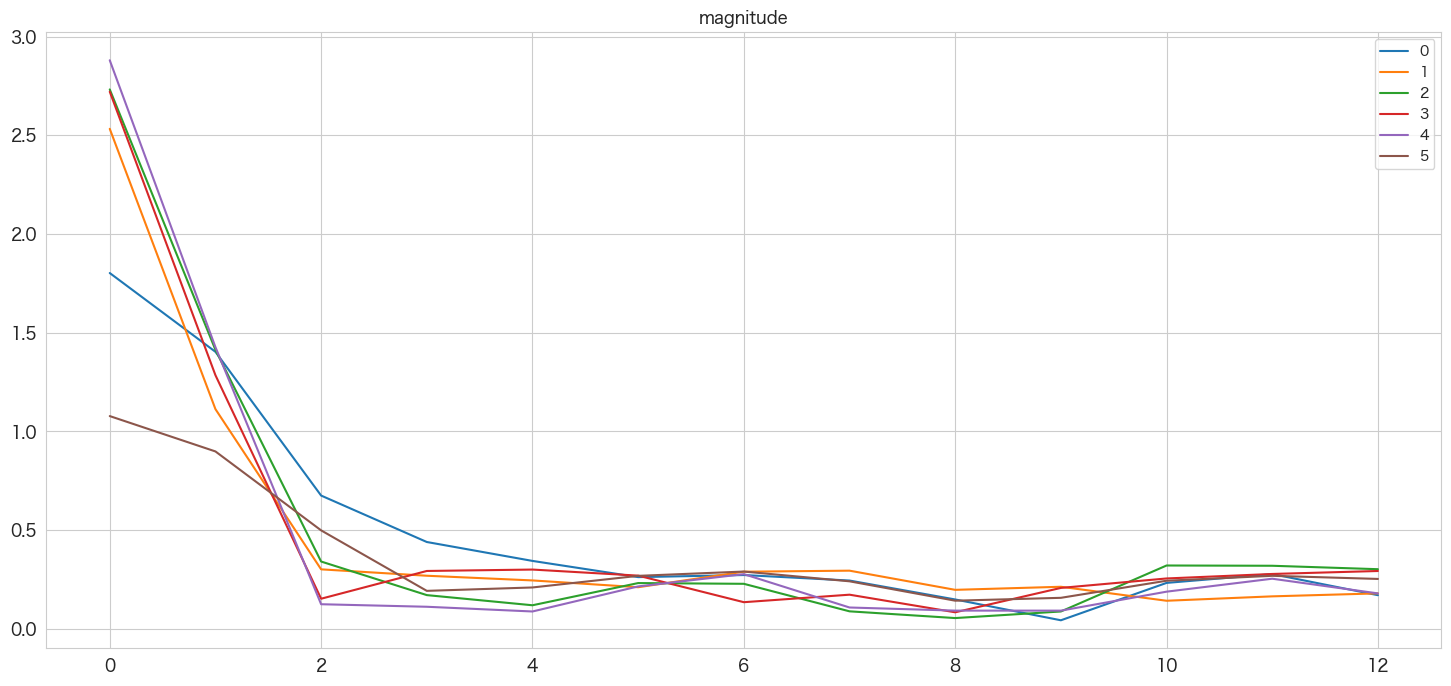
pd.DataFrame(np.abs(Zxx)).plot()
plt.title(col)
plt.show()
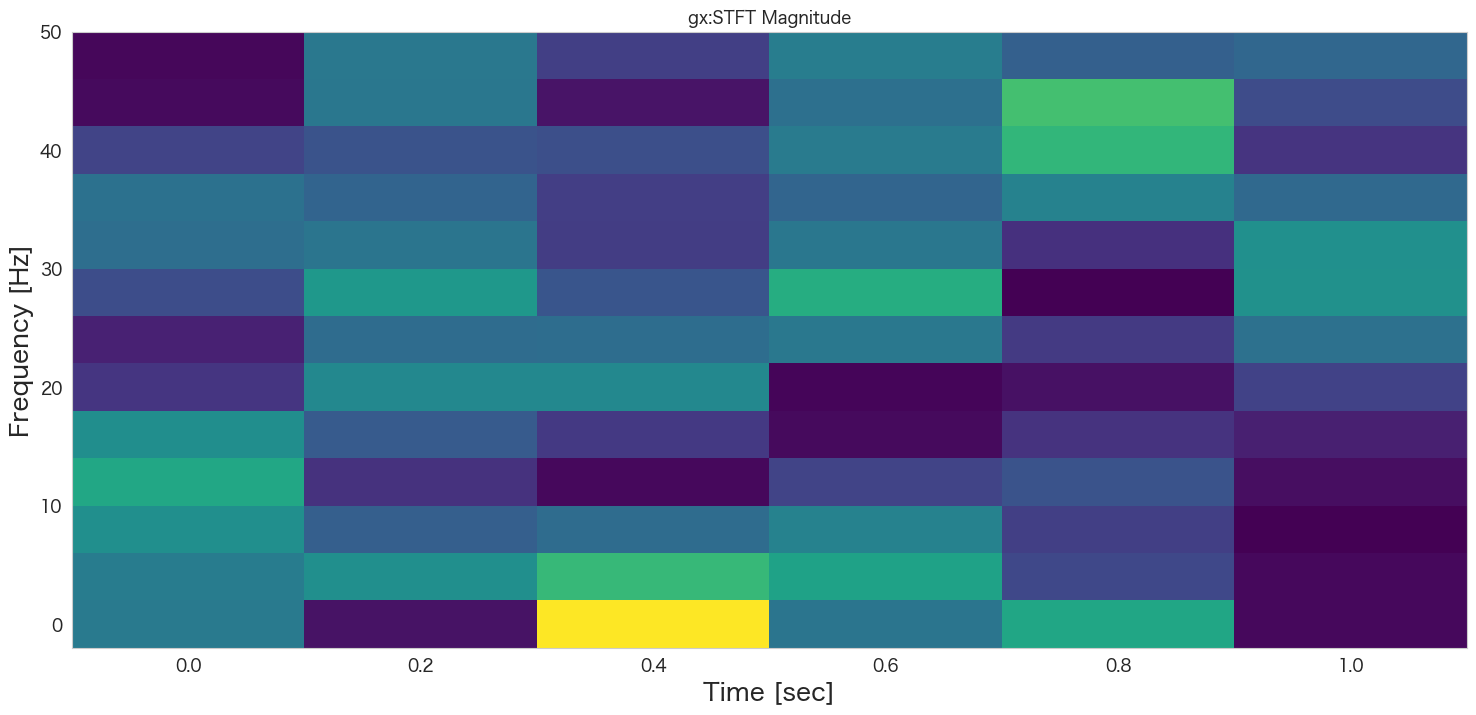
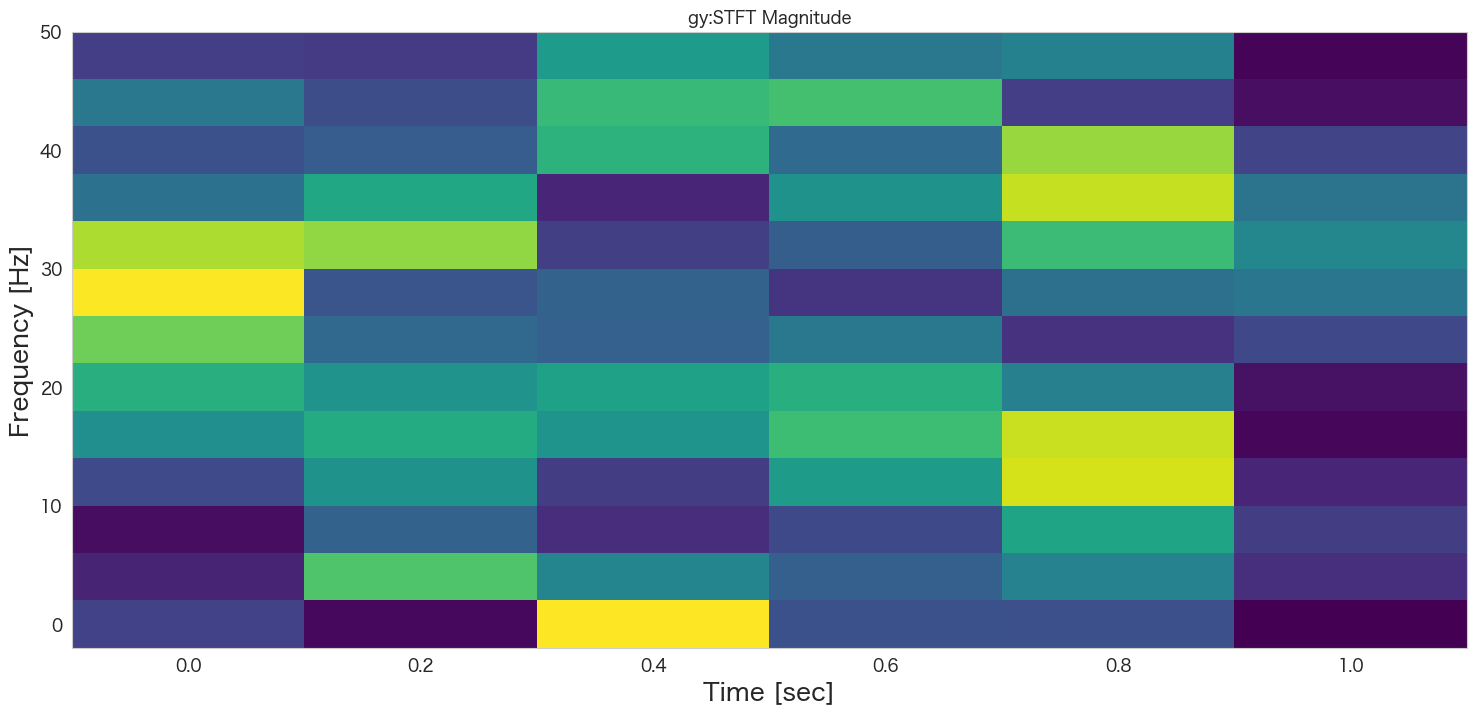
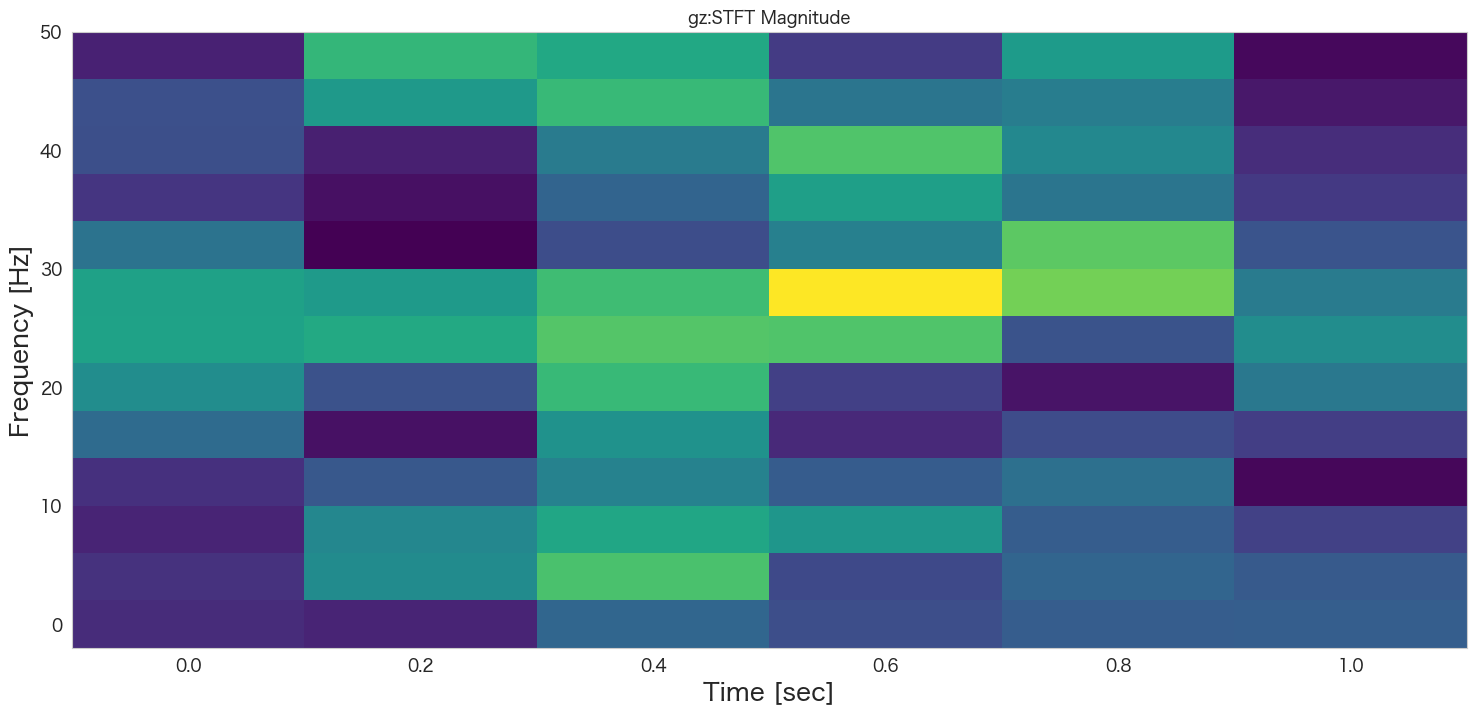
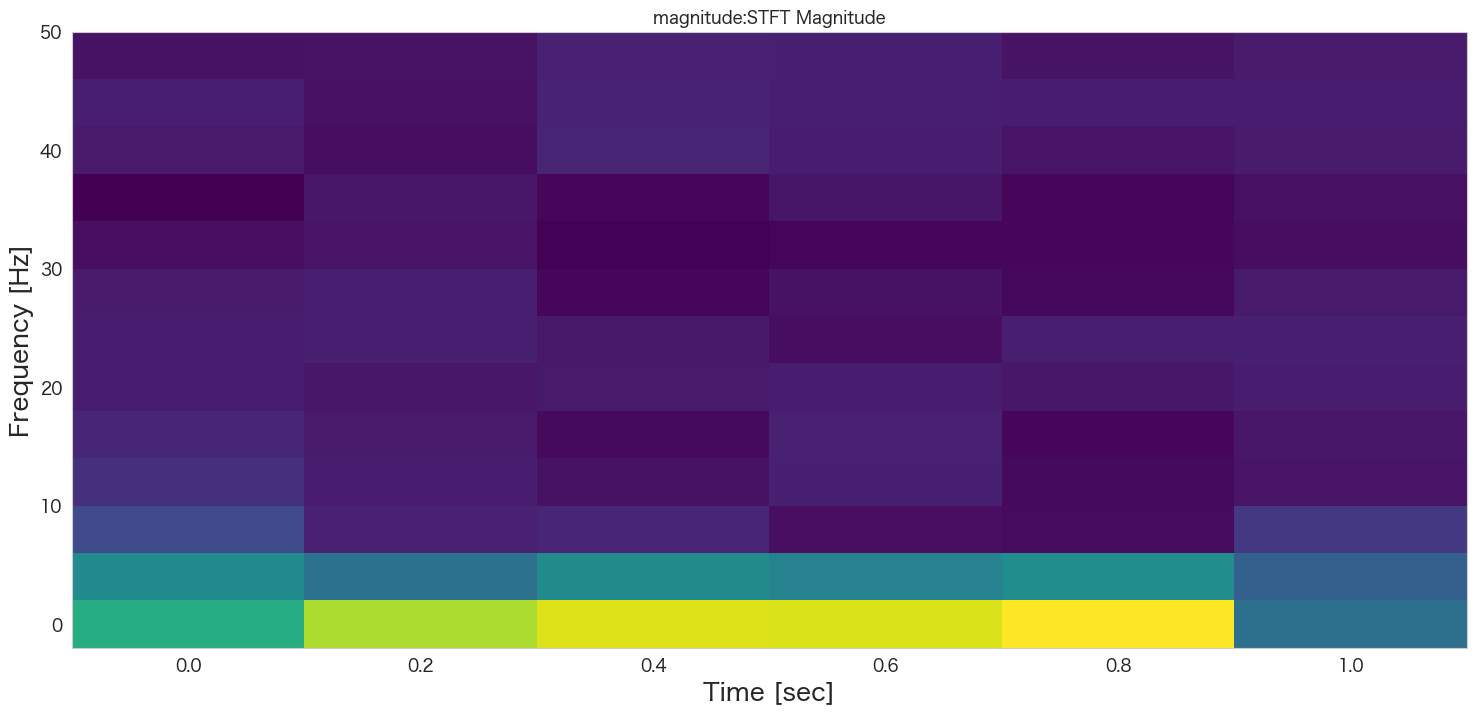
# グラフの描画
plt.pcolormesh(t, f, np.abs(Zxx), cmap='viridis')
plt.title(col+':STFT Magnitude')
plt.ylabel('Frequency [Hz]')
plt.xlabel('Time [sec]')
plt.show()
print(stft_result_dict)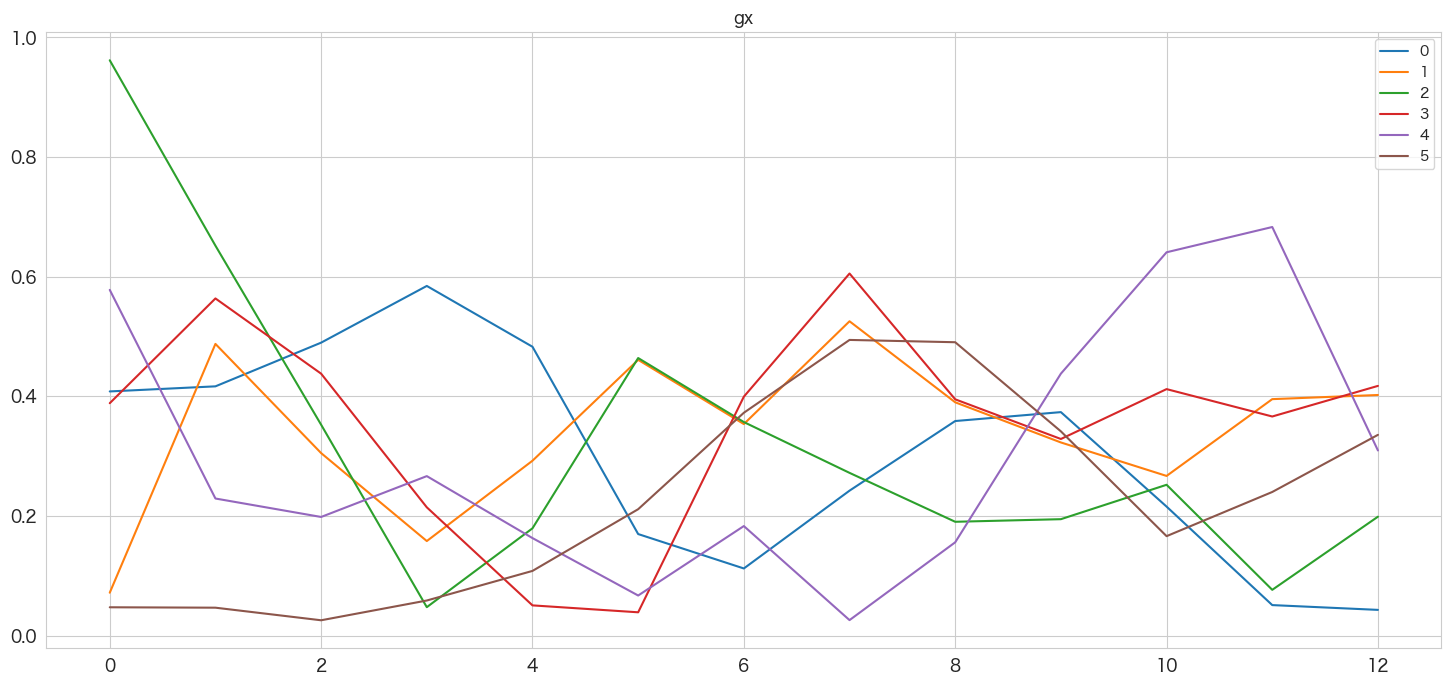
{'stft_gx': array([[0.40828839, 0.07186209, 0.96184552, 0.38862153, 0.57804924,
0.04748448],
[0.4167916 , 0.48772208, 0.65191552, 0.56372311, 0.22928645,
0.04679885],
[0.48982804, 0.30523565, 0.35266191, 0.43798449, 0.19844571,
0.02574956],
[0.58463169, 0.1581835 , 0.04766933, 0.21457477, 0.26674394,
0.05878624],
[0.48296954, 0.29245554, 0.17948346, 0.05065432, 0.16314131,
0.10827083],
[0.16987528, 0.46108078, 0.46410175, 0.03909534, 0.06713935,
0.21141395],
[0.112361 , 0.35373987, 0.35708962, 0.39954364, 0.18323934,
0.37262812],
[0.24242364, 0.52556292, 0.27216734, 0.60538101, 0.02603147,
0.49437673],
[0.35880868, 0.39010783, 0.19039732, 0.3951022 , 0.15609733,
0.49053051],
[0.37370319, 0.32298424, 0.19473788, 0.32879412, 0.43801864,
0.34155467],
[0.21578233, 0.26703647, 0.25224172, 0.41217194, 0.64088874,
0.16636606],
[0.05113309, 0.39539641, 0.07664232, 0.36638536, 0.68313697,
0.24021068],
[0.04313004, 0.40233206, 0.19891739, 0.4175427 , 0.30962707,
0.33570843]]), 'stft_gy': array([[0.16797086, 0.03119797, 0.78079749, 0.20437078, 0.20389728,
0.0157652 ],
[0.09199709, 0.57138105, 0.36419672, 0.24514333, 0.35619178,
0.1199268 ],
[0.04120896, 0.25239265, 0.11157069, 0.18334391, 0.46262136,
0.15052449],
[0.187597 , 0.40607264, 0.15249226, 0.43587446, 0.73257984,
0.09548191],
[0.39279981, 0.48255808, 0.41238592, 0.53891609, 0.71677825,
0.02902788],
[0.4969599 , 0.41009741, 0.45149664, 0.4980909 , 0.34589269,
0.05141102],
[0.61142573, 0.2727444 , 0.25030183, 0.32298286, 0.12368553,
0.18129648],
[0.77543237, 0.21463835, 0.25662122, 0.13240171, 0.29661337,
0.3158961 ],
[0.68764249, 0.6528943 , 0.15841867, 0.24256565, 0.53727741,
0.37013622],
[0.30393803, 0.47187788, 0.09362317, 0.40233416, 0.71248313,
0.3079928 ],
[0.2069513 , 0.2387134 , 0.50861517, 0.2782877 , 0.66399063,
0.17108934],
[0.32265425, 0.19214677, 0.53090324, 0.55239754, 0.15601371,
0.04469176],
[0.15401788, 0.14752866, 0.4322075 , 0.32123416, 0.34793026,
0.02312096]]), 'stft_gz': array([[0.1340738 , 0.11507169, 0.29619259, 0.2232988 , 0.26707108,
0.27132703],
[0.14879053, 0.41715726, 0.60493405, 0.2120556 , 0.29177252,
0.25884224],
[0.11400673, 0.40463081, 0.50654098, 0.45568653, 0.26744213,
0.19018736],
[0.14695149, 0.25108148, 0.38830546, 0.26479231, 0.32794748,
0.04748086],
[0.31062214, 0.07114674, 0.4409565 , 0.12646744, 0.21840489,
0.17870612],
[0.42421563, 0.23552763, 0.57266579, 0.1868673 , 0.0769267 ,
0.35439209],
[0.49444562, 0.51660356, 0.62202884, 0.61554665, 0.23952103,
0.42338014],
[0.49270839, 0.46869459, 0.5847629 , 0.83462074, 0.66539451,
0.36324049],
[0.33961213, 0.0345782 , 0.22036273, 0.37864339, 0.63354614,
0.24172959],
[0.15787776, 0.06822629, 0.29036586, 0.4825945 , 0.34653909,
0.16780484],
[0.22734538, 0.10437063, 0.36383797, 0.61306792, 0.40662777,
0.1355579 ],
[0.23097735, 0.46300208, 0.57351821, 0.34706581, 0.37176524,
0.08626509],
[0.10746879, 0.56430669, 0.51501492, 0.17237191, 0.47151397,
0.05294381]]), 'stft_magnitude': array([[1.80229574, 2.53262052, 2.73207458, 2.72069009, 2.87974611,
1.07781977],
[1.4033474 , 1.11308607, 1.41333313, 1.28488498, 1.42706774,
0.89880102],
[0.67531957, 0.30163234, 0.34122091, 0.15285343, 0.12498447,
0.49904228],
[0.44012493, 0.26926033, 0.17116164, 0.29343807, 0.11214273,
0.19269738],
[0.34433256, 0.24548637, 0.11973765, 0.30057412, 0.08825139,
0.20990132],
[0.26226581, 0.21117223, 0.23214976, 0.26982362, 0.21519618,
0.2687133 ],
[0.2728266 , 0.28968969, 0.22838936, 0.13527174, 0.27738215,
0.29049603],
[0.24492361, 0.29494258, 0.08898997, 0.17330594, 0.1084151 ,
0.24103783],
[0.14909215, 0.19785056, 0.05490826, 0.08413002, 0.09264984,
0.1428928 ],
[0.04370243, 0.21338329, 0.08823676, 0.20764166, 0.09248847,
0.15743987],
[0.23300615, 0.1425925 , 0.32111834, 0.25545493, 0.1885995 ,
0.24401086],
[0.2776563 , 0.16485498, 0.31978541, 0.27826012, 0.25419056,
0.26892122],
[0.17074262, 0.17995169, 0.30238523, 0.29329369, 0.17983603,
0.25307893]])}
データの正規化
異なる重量や物体から生み出される信号を比較可能にするためデータの正規化を行います。
例えば子供と大人では歩いたときや座ったときの加速度センサーの最大値は変わるはずです。
比較するため、異常値の影響を少なくするため、多くの場合で正規分布を仮定している機械学習のアルゴリズムに適用しやすくするためなどデータの正規化や標準化は広く使われる手法です。
0から1の間にスケールする方法や、平均が0で標準偏差を1にするように変換するする方法などがあります。
今回はscikit-learnのStandardScalerを使ってデータの平均を0、標準偏差を1にするように標準化してみようと思います。
元データ、乗数加速度、フーリエ変換済みデータ、ウェーブレット変換済みデータの正規化
# 変換対象のカラム名の確認
df.columns
Index(['gx', 'gy', 'gz', 'velocity', 'magnitude', 'fft_gx', 'fft_gy', 'fft_gz',
'fft_mag', 'wvlt_gx', 'wvlt_gy', 'wvlt_gz', 'wvlt_mag'],
dtype='object')
# 変換対象のカラム名の羅列
feature_cols=['gx', 'gy', 'gz', 'velocity', 'magnitude',
'fft_gx', 'fft_gy','fft_gz', 'fft_mag',
'wvlt_gx', 'wvlt_gy', 'wvlt_gz','wvlt_mag']
# 変換対象のデータの取得
features = df[feature_cols]
# 変換
scaler = StandardScaler()
scaled_features = scaler.fit_transform(features)
# 各カラムに_scaledをつける
new_feature_cols=list(map(lambda x: x+"_scaled", feature_cols))
df_scaled = pd.DataFrame(scaled_features, columns=new_feature_cols)
# 描画
df_scaled[["gx_scaled","gy_scaled","gz_scaled","magnitude_scaled"]].plot()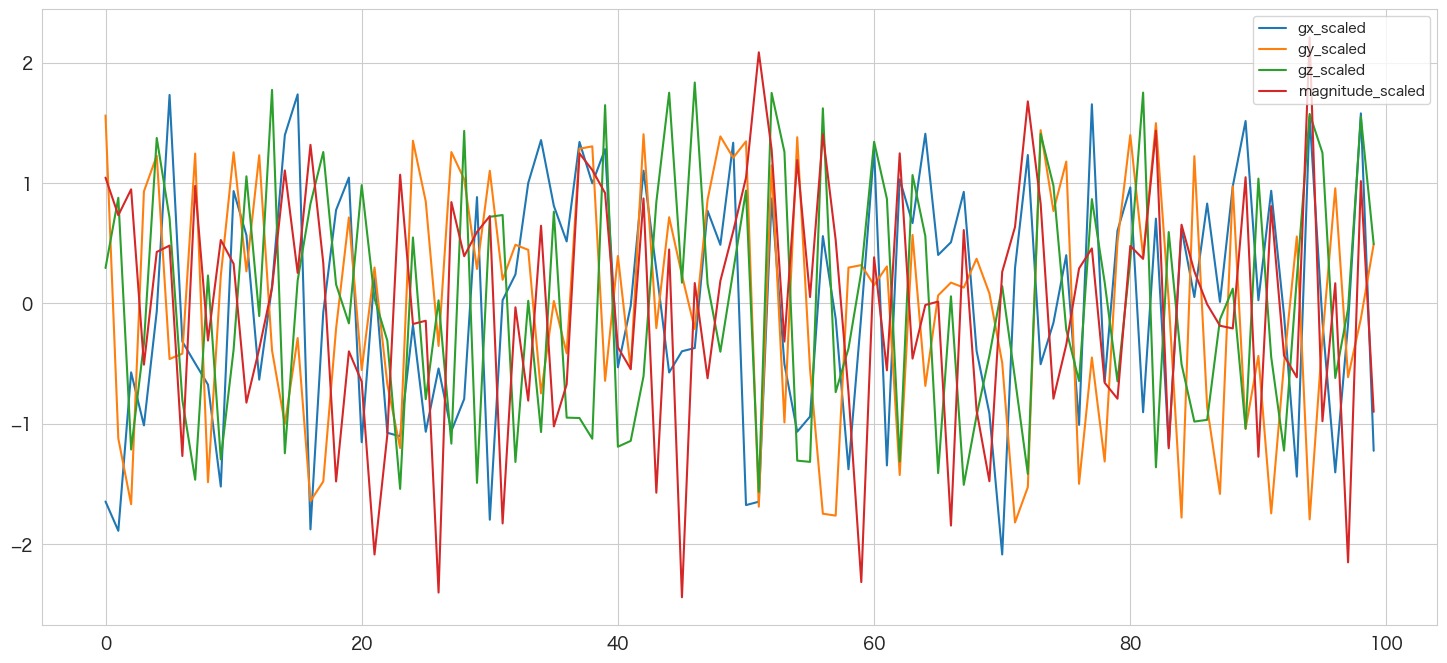
標準化したデータの確認 (平均=0、標準偏差=1になっているはず)
df_scaled.describe()
gx_scaled gy_scaled gz_scaled velocity_scaled magnitude_scaled fft_gx_scaled fft_gy_scaled fft_gz_scaled fft_mag_scaled wvlt_gx_scaled wvlt_gy_scaled wvlt_gz_scaled wvlt_mag_scaled count 1.000000e+02 1.000000e+02 1.000000e+02 1.000000e+02 1.000000e+02 1.000000e+02 1.000000e+02 1.000000e+02 1.000000e+02 1.000000e+02 1.000000e+02 1.000000e+02 1.000000e+02 mean -1.332268e-17 -3.164136e-17 -3.941292e-17 4.440892e-18 3.086420e-16 1.609823e-16 -7.327472e-17 1.842970e-16 -2.969847e-17 -2.220446e-18 -3.330669e-18 -2.220446e-18 7.271961e-17 std 1.005038e+00 1.005038e+00 1.005038e+00 1.005038e+00 1.005038e+00 1.005038e+00 1.005038e+00 1.005038e+00 1.005038e+00 1.005038e+00 1.005038e+00 1.005038e+00 1.005038e+00 min -2.087549e+00 -1.821533e+00 -1.566575e+00 -1.697657e+00 -2.443194e+00 -1.566465e+00 -1.738066e+00 -1.520074e+00 -3.442643e-01 -2.329652e+00 -2.423038e+00 -1.950267e+00 -1.980341e+00 25% -8.227170e-01 -6.513896e-01 -9.509892e-01 -9.186013e-01 -6.532869e-01 -6.299590e-01 -6.550037e-01 -6.390839e-01 -2.288535e-01 -7.625044e-01 -6.517022e-01 -8.561280e-01 -9.299939e-01 50% -4.650633e-03 1.409584e-01 3.234210e-02 -1.100051e-02 1.673747e-01 -2.157108e-01 -1.383770e-01 -1.444023e-01 -1.356966e-01 7.376064e-02 1.384773e-01 -1.105651e-01 -3.214357e-02 75% 8.743432e-01 8.779288e-01 8.469443e-01 8.178869e-01 7.264317e-01 5.814724e-01 6.303326e-01 4.472705e-01 1.134190e-02 6.735059e-01 6.775375e-01 8.402000e-01 9.045496e-01 max 1.736198e+00 1.561103e+00 1.834850e+00 1.744893e+00 2.210767e+00 3.317473e+00 2.044686e+00 3.776822e+00 9.825871e+00 2.338325e+00 2.049019e+00 2.133978e+00 1.841951e+00
ちゃんと標準化されているようです。
短時間フーリエ変換データの正規化
こちらもやっておきます。
stft_cols = ['stft_gx', 'stft_gy', 'stft_gz','stft_magnitude']
for col in stft_cols:
stft_result_dict[col+"_scaled"] = scaler.fit_transform(stft_result_dict[col])各種統計量の算出
全体の指標と特定の秒数毎に区切ったセグメント毎の指標を計算しようと思います。
短時間フーリエ変換したデータはすでに秒数を区切った指標になっているので、各セグメントごとの指標を計算します。
時間軸のセグメントの作成
全部で5つのセグメントを作成します。(5つは独断で決めました。)
segment_size = num_points // 5
# セグメントの作成
df['segment'] = np.floor(df.index / segment_size)
# 確認
df.groupby('segment').describe().T
segment 0.0 1.0 2.0 3.0 4.0 gx count 20.000000 20.000000 20.000000 20.000000 20.000000 mean 0.106102 0.290991 -0.008012 0.557239 0.545060 std 1.792647 1.564754 1.373754 1.578798 1.548214 min -2.640064 -2.497038 -2.308091 -2.945917 -1.940093 25% -0.883735 -1.354756 -0.737764 -0.543890 -0.252480 ... ... ... ... ... ... ... wvlt_mag min 2.278273 2.083420 -1.373968 -1.985965 -1.502931 25% 3.597375 3.243040 0.135348 -0.155466 -0.133439 50% 3.870822 3.900965 1.815226 0.479550 0.109574 75% 4.521043 4.512554 4.041739 0.968066 0.692114 max 5.192936 5.869938 4.707739 1.769212 1.952856 104 rows × 5 columns
平均やパーセンタイルなどの指標の作成
思いつく限り波形を説明できる変数を作成していきます。
ml_cols=['gx', 'gy', 'gz', 'velocity', 'magnitude', 'fft_gx', 'fft_gy',
'fft_gz', 'fft_mag', 'wvlt_gx', 'wvlt_gy', 'wvlt_gz', 'wvlt_mag']
ml_cols_scaled=['gx_scaled', 'gy_scaled', 'gz_scaled', 'velocity_scaled',
'magnitude_scaled', 'fft_gx_scaled', 'fft_gy_scaled', 'fft_gz_scaled',
'fft_mag_scaled', 'wvlt_gx_scaled', 'wvlt_gy_scaled', 'wvlt_gz_scaled',
'wvlt_mag_scaled']
ml_cols_stft=['stft_gx', 'stft_gy', 'stft_gz', 'stft_magnitude']
ml_cols_stft_scaled=['stft_gx_scaled', 'stft_gy_scaled', 'stft_gz_scaled', 'stft_magnitude_scaled']df_ml_stats=pd.DataFrame()
df_ml_pct=pd.DataFrame()
df_ml_pct_scaled=pd.DataFrame()
df_ml_cross_corr=pd.DataFrame()
df_ml_stft=pd.DataFrame()
df_ml_stft_scaled=pd.DataFrame()
df_ml_stft_corr=pd.DataFrame()
# 基礎統計情報
for col in ml_cols:
df_ml_stats[col+"_mean"] = [df[col].mean()]
df_ml_stats[col+"_std"] = [df[col].std()]
df_ml_stats[col+"_skew"] = [df[col].skew()]
df_ml_stats[col+"_kurt"] = [df[col].kurt()]
df_ml_stats[col+"_autocorr"] = [df[col].autocorr()]
# パーセンタイル
for col in ml_cols:
df_ml_pct[col+"_min"] = [df[col].min()]
df_ml_pct[col+"_25pct"] = [np.percentile(df[col],25)]
df_ml_pct[col+"_median"] = [np.percentile(df[col],50)]
df_ml_pct[col+"_75pct"] = [np.percentile(df[col],75)]
df_ml_pct[col+"_max"] = [df[col].max()]
# パーセンタイル(正規化したもの)
for col in ml_cols_scaled:
df_ml_pct_scaled[col+"_min"] = [df_scaled[col].min()]
df_ml_pct_scaled[col+"_25pct"] = [np.percentile(df_scaled[col],25)]
df_ml_pct_scaled[col+"_median"] = [np.percentile(df_scaled[col],50)]
df_ml_pct_scaled[col+"_75pct"] = [np.percentile(df_scaled[col],75)]
df_ml_pct_scaled[col+"_max"] = [df_scaled[col].max()]
# 相関係数
C = comb(ml_cols,2)
for col1,col2 in C:
df_ml_cross_corr[col1+"_"+col2+"_corr"] = [df[col1].corr(df[col2])]
# 短時間フーリエ変換データの統計量
_, stft_colnum = stft_result_dict["stft_gx"].shape
for col in stft_cols:
new_cols=[col + "_kbn" + str(idx) for idx in range(1, stft_colnum+1)]
df_ml_stft = pd.concat([df_ml_stft, pd.DataFrame(np.mean(stft_result_dict[col], axis=0).reshape(1,-1),columns=map(lambda x: x+"_mean", new_cols))],axis=1)
df_ml_stft = pd.concat([df_ml_stft, pd.DataFrame(np.min(stft_result_dict[col], axis=0).reshape(1,-1),columns=map(lambda x: x+"_min", new_cols))],axis=1)
df_ml_stft = pd.concat([df_ml_stft, pd.DataFrame(np.percentile(stft_result_dict[col], 25, axis=0).reshape(1,-1),columns=map(lambda x: x+"_25pct", new_cols))],axis=1)
df_ml_stft = pd.concat([df_ml_stft, pd.DataFrame(np.median(stft_result_dict[col], axis=0).reshape(1,-1),columns=map(lambda x: x+"_median", new_cols))],axis=1)
df_ml_stft = pd.concat([df_ml_stft, pd.DataFrame(np.percentile(stft_result_dict[col], 75, axis=0).reshape(1,-1),columns=map(lambda x: x+"_75pct", new_cols))],axis=1)
df_ml_stft = pd.concat([df_ml_stft, pd.DataFrame(np.max(stft_result_dict[col], axis=0).reshape(1,-1),columns=map(lambda x: x+"_max", new_cols))],axis=1)
# autocorrメソッド使いたいので別途やった。
for idx in range(stft_colnum):
df_ml_stft[col+"_kbn"+str(idx+1)+"_autocorr"] = pd.DataFrame(stft_result_dict[col])[idx].autocorr()
# 短時間フーリエ変換データの統計量 (正規化したものから四分位)
for col in ml_cols_stft_scaled:
new_cols=[col + "_kbn" + str(idx) for idx in range(1, stft_colnum+1)]
df_ml_stft_scaled = pd.concat([df_ml_stft_scaled, pd.DataFrame(np.min(stft_result_dict[col], axis=0).reshape(1,-1),columns=map(lambda x: x+"_min", new_cols))],axis=1)
df_ml_stft_scaled = pd.concat([df_ml_stft_scaled, pd.DataFrame(np.percentile(stft_result_dict[col], 25, axis=0).reshape(1,-1),columns=map(lambda x: x+"_25pct", new_cols))],axis=1)
df_ml_stft_scaled = pd.concat([df_ml_stft_scaled, pd.DataFrame(np.median(stft_result_dict[col], axis=0).reshape(1,-1),columns=map(lambda x: x+"_median", new_cols))],axis=1)
df_ml_stft_scaled = pd.concat([df_ml_stft_scaled, pd.DataFrame(np.percentile(stft_result_dict[col], 75, axis=0).reshape(1,-1),columns=map(lambda x: x+"_75pct", new_cols))],axis=1)
df_ml_stft_scaled = pd.concat([df_ml_stft_scaled, pd.DataFrame(np.max(stft_result_dict[col], axis=0).reshape(1,-1),columns=map(lambda x: x+"_max", new_cols))],axis=1) # 短時間フーリエ変換データの相関係数 (時間区分毎)
# 各変数は6つの時間区分の情報を持つため、すべて横に結合して1つにする。
df_ml_stft_corr = pd.concat([pd.DataFrame(stft_result_dict["stft_gx"])
,pd.DataFrame(stft_result_dict["stft_gy"])
,pd.DataFrame(stft_result_dict["stft_gz"])
,pd.DataFrame(stft_result_dict["stft_magnitude"])
],axis=1)
# カラム名の付与
df_ml_stft_corr.columns = [col + "_kbn" + str(idx) for col in ml_cols_stft for idx in range(1, 7)]
# 相関係数の計算。行列で返ってくる
result_matrix = df_ml_stft_corr.corr()
# 行列からリストに変換する (同じ変数同士と同じ組み合わせの変数は除外)
stacked_corr = result_matrix.stack()
corr_df = stacked_corr.reset_index()
corr_df.columns = ['col1', 'col2', 'corr']
# 同じカラム名は除外
corr_df = corr_df[corr_df['col1'] != corr_df['col2']]
# 同じ組み合わせのカラムは除外
corr_df['sorted_col_name'] = corr_df[['col1', 'col2']].apply(lambda x: '_'.join(sorted(x)), axis=1)
corr_df = corr_df.drop_duplicates(subset='sorted_col_name')
# 横持ち変換
df_ml_stft_corr = pd.DataFrame(corr_df["corr"].to_numpy().reshape(1,-1),columns=map(lambda x: x+"_corr", list(corr_df.sorted_col_name)))大変でした。。最終的に変数選択でほとんど落とされると思いますが、思いつく限り作成しています。
計算した統計量のデータフレームたちの結合
最初から1つの大きなデータフレームを作ろうと思ったのですが、df["追加したい変数"] = values で変数を追加していくと下記PerformanceWarningが発生しました。
/var/folders/n0/ft3172td6v70d6klgt216_3r0000gn/T/ipykernel_97662/3636255042.py:13: PerformanceWarning: DataFrame is highly fragmented. This is usually the result of calling
frame.insertmany times, which has poor performance. Consider joining all columns at once using pd.concat(axis=1) instead.
従って、いくつかのデータフレームに分けて最終的にpd.concatするという方法にしました。
# 作成した全てのデータフレームを結合する
final_output = pd.concat([df_ml_stats
,df_ml_pct
,df_ml_pct_scaled
,df_ml_cross_corr
,df_ml_stft
,df_ml_stft_scaled
,df_ml_stft_corr
], axis=1)
final_output
gx_mean gx_std gx_skew gx_kurt gx_autocorr gy_mean gy_std gy_skew gy_kurt gy_autocorr ... stft_magnitude_kbn2_stft_magnitude_kbn3_corr stft_magnitude_kbn2_stft_magnitude_kbn4_corr stft_magnitude_kbn2_stft_magnitude_kbn5_corr stft_magnitude_kbn2_stft_magnitude_kbn6_corr stft_magnitude_kbn3_stft_magnitude_kbn4_corr stft_magnitude_kbn3_stft_magnitude_kbn5_corr stft_magnitude_kbn3_stft_magnitude_kbn6_corr stft_magnitude_kbn4_stft_magnitude_kbn5_corr stft_magnitude_kbn4_stft_magnitude_kbn6_corr stft_magnitude_kbn5_stft_magnitude_kbn6_corr 0 0.298276 1.561897 -0.146861 -1.006716 0.03148 0.188684 1.755063 -0.25248 -1.033696 -0.003628 ... 0.982822 0.989354 0.989965 0.913242 0.990148 0.995074 0.947813 0.992809 0.90994 0.930387 1 rows × 837 columns
まとめ
機械学習投入用のデータを作成しました。最終的に4変数が837変数になりました。
本当でしたら移動平均なども作成した方が良かったかも知れませんが別の機会とすることにします。
時間があるときに加速度センサーのデータを自分自身で取得し、アクティビティを分類したいですね。