評価指標
住宅IdごとのSalePrice(販売価格)を予測するコンペです。
評価指標は予測SalePriceと実測SalePriceの対数を取ったRoot-Mean-Squared-Error(RMSE)の値のようです。
House Prices - Advanced Regression Techniques | Kaggle
Predict sales prices and practice feature engineering, RFs, and gradient boosting
www.kaggle.com
単回帰分析
分析用データの準備
事前に欠損値処理や特徴量エンジニアリングを実施してデータをエクスポートしています。
本記事と同じ結果にするためには事前に下記記事を確認してデータを用意してください。
(その3-2) エイムズの住宅価格のデータセットのデータ加工①
(その3-3) エイムズの住宅価格のデータセットのデータ加工②
学習用データとスコア付与用データの読み込み
import pandas as pd
# エイムズの住宅価格のデータセットの訓練データとテストデータを読み込む
df = pd.read_csv("/Users/hinomaruc/Desktop/blog/dataset/ames/ames_train.csv")
df_test = pd.read_csv("/Users/hinomaruc/Desktop/blog/dataset/ames/ames_test.csv")df.head()Out[0]
Id LotFrontage LotArea LotShape Utilities LandSlope OverallQual OverallCond MasVnrArea ExterCond ... SaleType_New SaleType_Oth SaleType_WD SaleCondition_Abnorml SaleCondition_AdjLand SaleCondition_Alloca SaleCondition_Family SaleCondition_Normal SaleCondition_Partial SalePrice 0 1 65.0 8450 3.0 3.0 2.0 7 5 196.0 2.0 ... 0.0 0.0 1.0 0.0 0.0 0.0 0.0 1.0 0.0 208500 1 2 80.0 9600 3.0 3.0 2.0 6 8 0.0 2.0 ... 0.0 0.0 1.0 0.0 0.0 0.0 0.0 1.0 0.0 181500 2 3 68.0 11250 2.0 3.0 2.0 7 5 162.0 2.0 ... 0.0 0.0 1.0 0.0 0.0 0.0 0.0 1.0 0.0 223500 3 4 60.0 9550 2.0 3.0 2.0 7 5 0.0 2.0 ... 0.0 0.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 140000 4 5 84.0 14260 2.0 3.0 2.0 8 5 350.0 2.0 ... 0.0 0.0 1.0 0.0 0.0 0.0 0.0 1.0 0.0 250000 5 rows × 335 columns
# 描画設定
import seaborn as sns
from matplotlib import ticker
import matplotlib.pyplot as plt
sns.set_style("whitegrid")
from matplotlib import rcParams
rcParams['font.family'] = 'Hiragino Sans' # Macの場合
#rcParams['font.family'] = 'Meiryo' # Windowsの場合
#rcParams['font.family'] = 'VL PGothic' # Linuxの場合
rcParams['xtick.labelsize'] = 12 # x軸のラベルのフォントサイズ
rcParams['ytick.labelsize'] = 12 # y軸のラベルのフォントサイズ
rcParams['axes.labelsize'] = 18 # ラベルのフォントとサイズ
rcParams['figure.figsize'] = 18,8 # 画像サイズの変更(inch)単回帰に使用する変数を選ぶ
なるべく目的変数と関係している変数を選びたいので、データ加工の時にもやったピアソンの相関係数とスピアマンの順位相関係数を算出してみようと思います。
ピアソンの相関係数 (目的変数との相関が0.5以上)
import numpy as np
# 相関係数を計算
corr = df.corr()
# マスク対象の行列をTrueにした行列を作成
np_for_mask = np.tril(np.ones(corr.shape)).astype(np.bool_)
# 相関行列の左下半分をnullに変換
corr = corr.mask(np_for_mask)
# 行列ではなく縦持ちに変換する
corr = corr.stack().reset_index()
corr.columns = ["col1","col2","r"]
corr[(abs(corr["r"]) >= 0.5) & (corr["col2"] == 'SalePrice')].sort_values(by="r",key=abs,ascending=False).reset_index().drop("index",axis=1)Out[0]
col1 col2 r 0 OverallQual SalePrice 0.790982 1 TotalLivArea SalePrice 0.778959 2 GarageCars SalePrice 0.640409 3 TotalBathRms SalePrice 0.613005 4 BsmtQual SalePrice 0.585207 5 FullBath SalePrice 0.560664 6 GarageFinish SalePrice 0.549247 7 TotRmsAbvGrd SalePrice 0.533723 8 FireplaceQu SalePrice 0.520438
スピアマンの順位相関係数 (目的変数との相関が0.5以上)
# 相関係数を計算
corr = df.corr(method='spearman')
# マスク対象の行列をTrueにした行列を作成
np_for_mask = np.tril(np.ones(corr.shape)).astype(np.bool_)
# 相関行列の左下半分をnullに変換
corr = corr.mask(np_for_mask)
# 行列ではなく縦持ちに変換する
corr = corr.stack().reset_index()
corr.columns = ["col1","col2","r"]
corr[(abs(corr["r"]) >= 0.5) & (corr["col2"] == 'SalePrice')].sort_values(by="r",key=abs,ascending=False).reset_index().drop("index",axis=1)Out[0]
col1 col2 r 0 TotalLivArea SalePrice 0.814984 1 OverallQual SalePrice 0.809829 2 TotalBathRms SalePrice 0.691160 3 GarageCars SalePrice 0.690711 4 BsmtQual SalePrice 0.678026 5 FullBath SalePrice 0.635957 6 GarageFinish SalePrice 0.633974 7 Foundation_PConc SalePrice 0.562287 8 FireplaceQu SalePrice 0.537602 9 TotRmsAbvGrd SalePrice 0.532586
ピアソンとスピアマンで若干結果が異なりますが、概ね傾向は同じようです。
# SalePriceと相関が高かった変数一覧
chk_cols=[
'TotalLivArea'
,'OverallQual'
,'TotalBathRms'
,'GarageCars'
,'BsmtQual'
,'FullBath'
,'GarageFinish'
,'Foundation_PConc'
,'FireplaceQu'
,'TotRmsAbvGrd'
,'SalePrice'
]
# 目的変数と相関が高い変数の関係性を視覚化
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(18,40))
for index in range(len(df[chk_cols].columns)):
plt.subplot(10,4,index+1)
sns.histplot(data=df[chk_cols],x=df[chk_cols].iloc[:,index],y="SalePrice",bins=20)
fig.tight_layout(pad=1.0)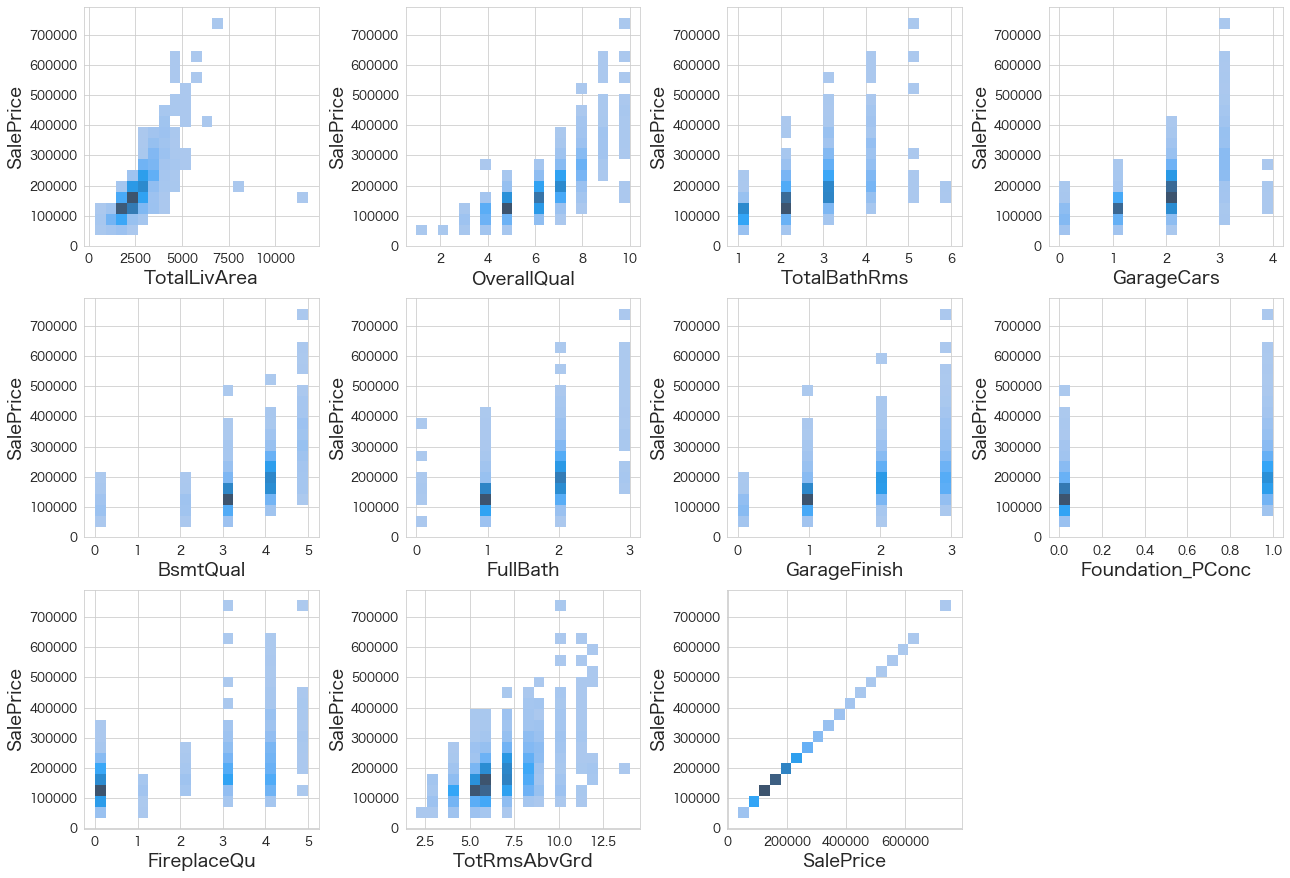
TotalLivAreaが広くなるとSalePriceも上がる傾向にありそうなので、TotalLivAreaでSalePriceを予測してみようと思います。
単回帰で学習を実施
# 説明変数と目的変数を指定
X_train = df["TotalLivArea"].values.reshape(-1,1) # 総住居面積
Y_train = df["SalePrice"] # 販売価格# モデル作成
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train,Y_train)Out[0]
LinearRegression()
単回帰結果の確認
# 説明変数の係数を確認
coef = pd.DataFrame()
coef["features"] = ['TotalLivArea']
coef["coef"] = model.coef_
coef["coef_pct"] = np.abs(coef["coef"]) / np.abs(coef["coef"]).sum()
coef.sort_values(by="coef_pct",ascending=False)Out[0]
features coef coef_pct 0 TotalLivArea 75.136659 1.0
model.intercept_Out[0]
-12397.399248388247
y = 75.13 * TotalLivArea - 12397.3 という式が完成しました。
住居面積によってはマイナスの価格になってしまいますね 笑
モデルを適用し、SalePriceの予測をする
# SalePriceを予測する
df_test["SalePrice"] = model.predict(df_test["TotalLivArea"].values.reshape(-1,1))# 予測結果の確認
df_test[["Id","TotalLivArea","SalePrice"]]Out[0]
Id TotalLivArea SalePrice 0 1461 1778.0 121195.580338 1 1462 2658.0 187315.840200 2 1463 2557.0 179727.037648 3 1464 2530.0 177698.347857 4 1465 2560.0 179952.447625 ... ... ... ... 1454 2915 1638.0 110676.448087 1455 2916 1638.0 110676.448087 1456 2917 2448.0 171537.141824 1457 2918 1882.0 129009.792867 1458 2919 2996.0 212712.030920 1459 rows × 3 columns
予測できていそうです。
Kaggleにスコア付与結果をアップロード
df_test[["Id","SalePrice"]].to_csv("ames_submission.csv",index=False)!/Users/hinomaruc/Desktop/blog/my-venv/bin/kaggle competitions submit -c house-prices-advanced-regression-techniques -f ames_submission.csv -m "#1 linear regression"Out[0]
100%|██████████████████████████████████████| 33.6k/33.6k [00:04<00:00, 8.33kB/s]
Successfully submitted to House Prices - Advanced Regression Techniques
#1 linear regression 0.24885
ランクは下の方でしたが、最下位ではありませんでした 笑
この数値を基準に他の機械学習も試していこうと思います。AutoMLが一番になる気はしています。
使用ライブラリのバージョン
pandas Version: 1.4.3
numpy Version: 1.22.4
scikit-learn Version: 1.1.1
seaborn Version: 0.11.2
matplotlib Version: 3.5.2
まとめ
単回帰ですが、結果はそれなりでした。
次回は重回帰分析を試したいと思います。結果が分かりやすいし、システムにも組み込みやすいので数値予測で私はよく使っています。
