(その1) US国際線乗客数の月次予測を自己回帰(AR)モデルでやってみた

時系列データ分析の第二弾です。10月中に投稿できてよかったです。(ハロウィーンですね)

前回はアップル引っ越しセンターのデータを使って、引っ越し数の日次予測に取り組みました。

apple-hikkoshi

「apple-hikkoshi」の記事一覧です。

www.hinomaruc.com

結果はProphet一択という感じになってしまいましたが、SARIMAモデルなどの実力はこんなものではないだろうということで今回はオーソドックスな時系列データを使って分析をしていきたいと思います。

今回利用するデータは1949年1月から1960年12月の期間内における、アメリカの国際線乗客者数の月次推移データになります。

元データのソースは「Box and Jenkins (1976): Times Series Analysis: Forecasting and Control, p. 531」になります。

よく時系列分析の勉強をしていると出てきていたデータになるのでこちらを先にこちらのデータで時系列モデルを試してみた方が良かったですね　笑

csvデータは色々なところでダウンロード出来るようですが、seabornで用意されているデータセットにありましたのでそちらを利用していこうと思います。

詳細情報はないのですが、中身をみるとBox and Jenkinsのair passengersのデータだと分かります。

seaborn-data/flights.csv at master · mwaskom/seaborn-data

Data repository for seaborn examples. Contribute to mwaskom/seaborn-data development by creating an account on GitHub.

github.com

乗客数の数は千人単位に丸められているようです。参考: mathematicaの時系列機能

それではまずはデータの中身から俯瞰していこうと思います。seabornを使いますのでインストールしていない方は pip install seabornが必要になります。

seabornのflightsデータの確認

# 描画設定
from IPython.display import HTML
import seaborn as sns
from matplotlib import ticker
import matplotlib.pyplot as plt
sns.set_style("whitegrid")
from matplotlib import rcParams
rcParams['font.family'] = 'Hiragino Sans' # Macの場合
#rcParams['font.family'] = 'Meiryo' # Windowsの場合
#rcParams['font.family'] = 'VL PGothic' # Linuxの場合
rcParams['xtick.labelsize'] = 12       # x軸のラベルのフォントサイズ
rcParams['ytick.labelsize'] = 12       # y軸のラベルのフォントサイズ
rcParams['axes.labelsize'] = 18        # ラベルのフォントとサイズ
rcParams['figure.figsize'] = 18,8      # 画像サイズの変更(inch)

# データの読み込み
flights = sns.load_dataset("flights")

# infoメソッドで基礎情報を確認
flights.info()

RangeIndex: 144 entries, 0 to 143
Data columns (total 3 columns):
 #   Column      Non-Null Count  Dtype   
---  ------      --------------  -----   
 0   year        144 non-null    int64   
 1   month       144 non-null    category
 2   passengers  144 non-null    int64   
dtypes: category(1), int64(2)
memory usage: 2.9 KB

# 上から5件を確認
flights.head()

  

    

      

      
year
      
month
      
passengers
    
  
  

    

      
0
      
1949
      
Jan
      
112
    
    

      
1
      
1949
      
Feb
      
118
    
    

      
2
      
1949
      
Mar
      
132
    
    

      
3
      
1949
      
Apr
      
129
    
    

      
4
      
1949
      
May
      
121
    
  

データの描画

# 乗客数を描画してみる ①
flights.passengers.plot()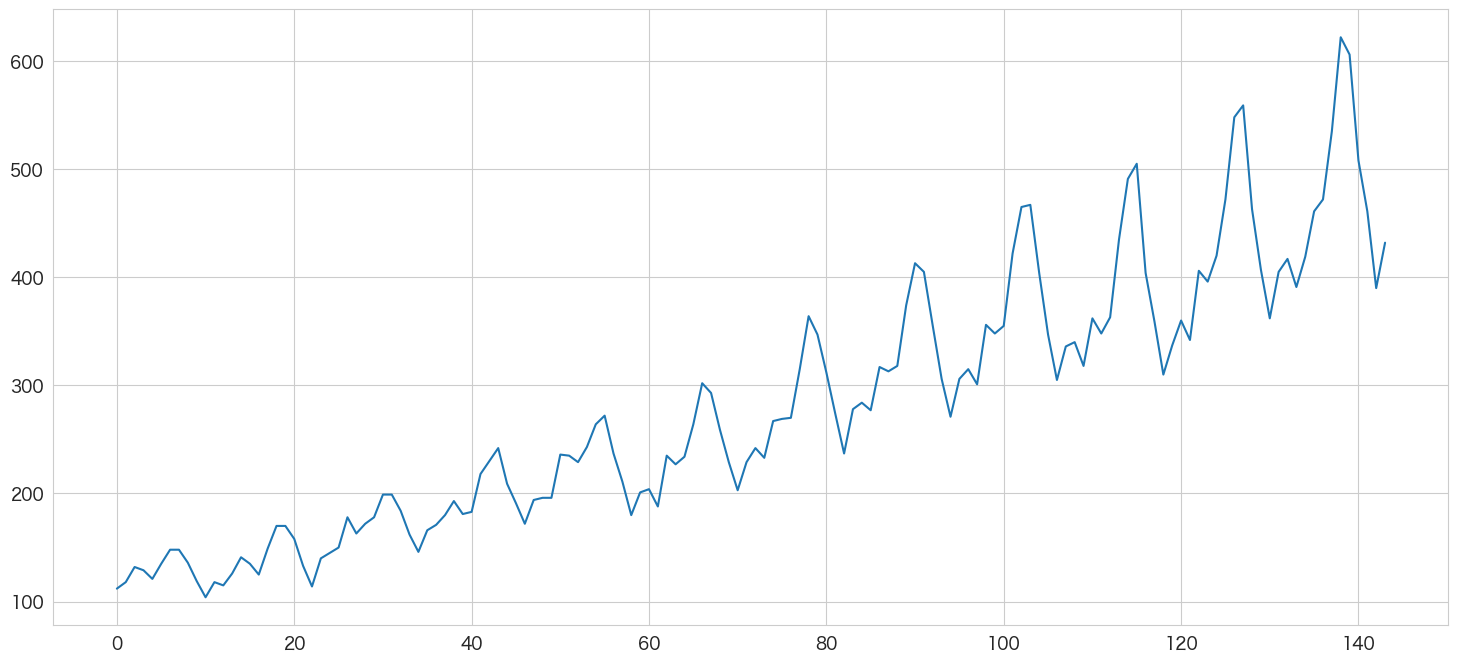

# 乗客数を描画してみる ②
sns.relplot(data=flights, x="month", y="passengers", hue="year", kind="line")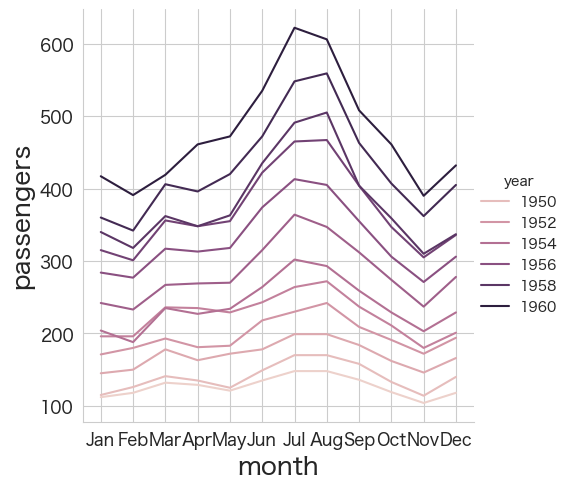

# 乗客数を描画してみる ③

# 各年度ごとの乗客数推移をプロット
g = sns.relplot(
    data=flights,
    x="month", y="passengers", col="year", hue="year",
    kind="line", palette="crest", linewidth=4, zorder=5,
    col_wrap=3, height=2, aspect=1.5, legend=False,
)

# 他の年度も一緒にプロットし目立たないように表示
for year, ax in g.axes_dict.items():

    sns.lineplot(
        data=flights, x="month", y="passengers", units="year",
        estimator=None, color=".7", linewidth=1, ax=ax,
    )

# X軸のラベルの表示を減らす
ax.set_xticks(ax.get_xticks()[::2])

# X軸の名称(month)を非表示
g.set_axis_labels("", "Passengers")
g.tight_layout()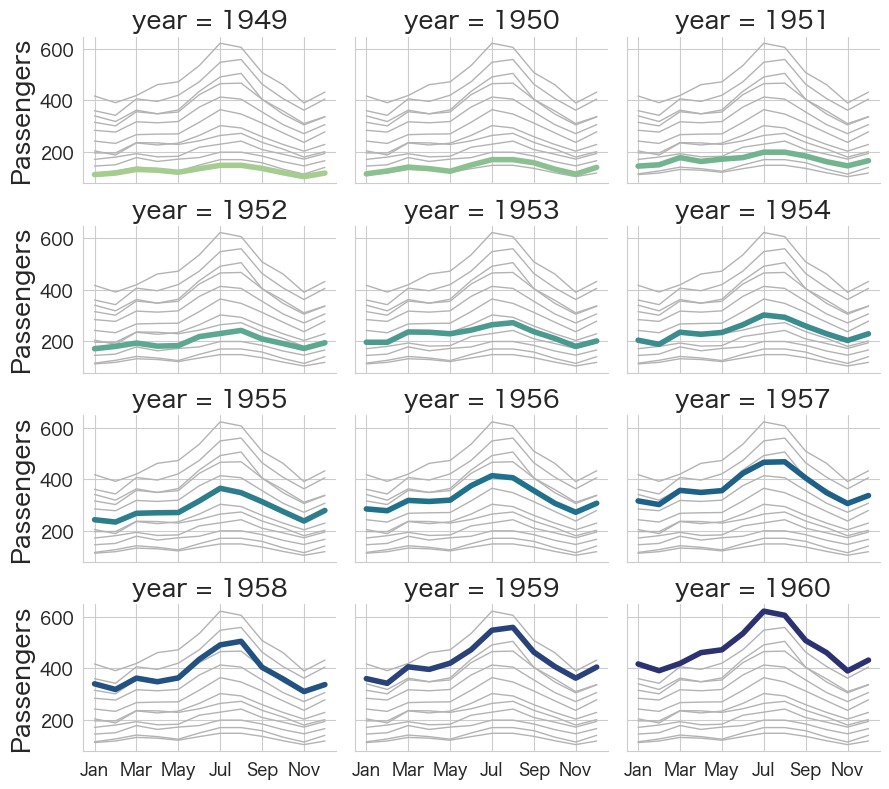

USの国際線乗客数をARモデルで予想する

データの読み込みと変換

import pandas as pd
# データの読み込み (既に読み込み済みだが、読みやすさのためもう一度実行する)
flights = sns.load_dataset("flights")
# 日付変換用カラムの作成
flights["date"] = flights.year.astype('str') + "-" + flights.month.astype('str')
# 日付カラムの作成
flights["ds"] =  pd.to_datetime(flights["date"], format="%Y-%b")
# datetimeをindexに設定、目的変数の型をfloat64に変換
flights = flights.set_index('ds').astype({'passengers': 'float64'}).drop(["date"], axis=1)
# 日付の間隔をasfreqメソッドで変更する
flights = flights.asfreq('MS')

# 基礎情報の確認
flights.info()

DatetimeIndex: 144 entries, 1949-01-01 to 1960-12-01
Freq: MS
Data columns (total 3 columns):
 #   Column      Non-Null Count  Dtype   
---  ------      --------------  -----   
 0   year        144 non-null    int64   
 1   month       144 non-null    category
 2   passengers  144 non-null    float64 
dtypes: category(1), float64(1), int64(1)
memory usage: 3.9 KB

日付をindexにしつつ、月次データであることを示すFreq: MSを設定することができました。

# データの中身を確認
flights

  

    

      

      
year
      
month
      
passengers
    
    

      
ds
      

      

      

    
  
  

    

      
1949-01-01
      
1949
      
Jan
      
112.0
    
    

      
1949-02-01
      
1949
      
Feb
      
118.0
    
    

      
1949-03-01
      
1949
      
Mar
      
132.0
    
    

      
1949-04-01
      
1949
      
Apr
      
129.0
    
    

      
1949-05-01
      
1949
      
May
      
121.0
    
    

      
...
      
...
      
...
      
...
    
    

      
1960-08-01
      
1960
      
Aug
      
606.0
    
    

      
1960-09-01
      
1960
      
Sep
      
508.0
    
    

      
1960-10-01
      
1960
      
Oct
      
461.0
    
    

      
1960-11-01
      
1960
      
Nov
      
390.0
    
    

      
1960-12-01
      
1960
      
Dec
      
432.0
    
  

144 rows × 3 columns

passengersが正規分布に従うかどうかQQプロットを確認

統計手法を適用するにあたり、おおよそ正規分布を仮定する必要があります。

そのためデータが正規分布に従っているかどうかQQプロットという手法を使って確認します。

# 正規分布に従うかどうかをQQプロットを描画して確認
import scipy.stats as stats
import matplotlib.pyplot as plt

plt.subplot(1,2,1)
sns.histplot(flights["passengers"], kde=True)
plt.subplot(1,2,2)
stats.probplot(flights["passengers"], dist="norm", plot=plt)
plt.show()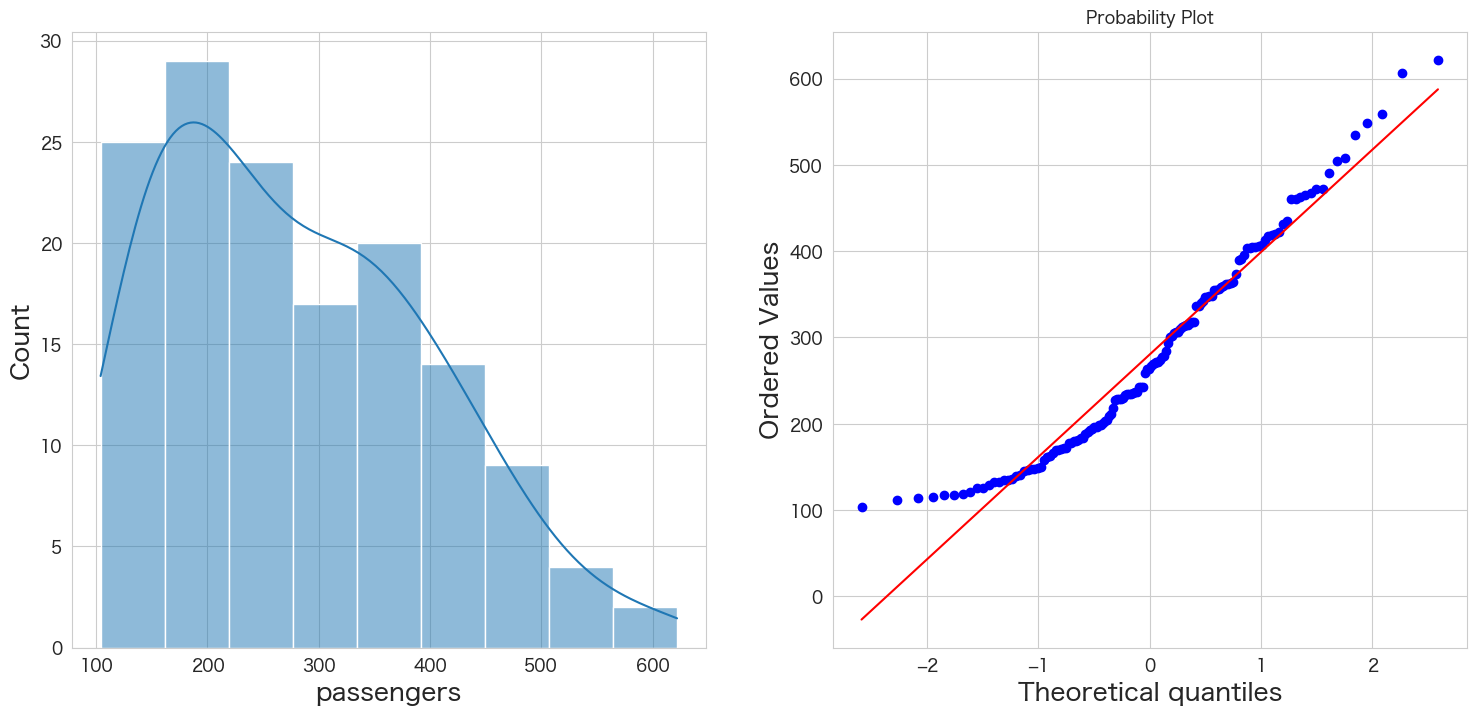

左側のグラフがヒストグラム、右側のグラフがQQプロットです。

青い点が赤い線に沿っていれば正規分布であるという表現方法になっています。

端の部分がずれているようですが、なんとなく正規分布に従っていると仮定しようと思います。

もし正規分布に明らかに従っていない場合は対数を取ったりBoxCox変換することによって正規性を担保できる可能性があります。

変数の変換に関してはpower-transform-time-series-forecast-data-pythonの記事が参考になるかと思います。

Mann-Kendall trend検定

まずはデータにトレンドが存在するか存在しないかをテストしてみたいと思います。

次の拡張ディッキー・フラー検定をする時にregressionの設定でtrendを含めるかどうかのオプションがあるので、Mann-Kendall trend検定でtrendが存在するという結果になれば、trendも考慮した拡張ディッキー・フラー検定してみようと思います。

How to Perform a Mann-Kendall Trend Test in Python

This tutorial explains how to perform a Mann-Kendall trend test in Python, including examples.

www.statology.org

H0: データにトレンドは存在しない
HA: データにトレンドが存在する

# https://pypi.org/project/pymannkendall/
import pymannkendall as mk
mk.original_test(flights["passengers"])

Mann_Kendall_Test(trend='increasing', h=True, p=0.0, z=14.381610025544802, Tau=0.8087606837606838, s=8327.0, var_s=335164.3333333333, slope=2.451216287678477, intercept=90.23803543098887)

p <= 0.05なので帰無仮説は棄却され、データにトレンドは存在するという結果になりました。また、trend='increasing'なので上昇トレンドのデータのようです。

そのため、拡張ディッキー・フラー検定ではregression='ct'のオプションを追加しようと思います。

拡張ディッキー・フラー検定で時系列データが(弱)定常か非定常か確認する

帰無仮説と対立仮説は下記です。

H0: 単位根がある
HA: 単位根がない

単位根についてはこちらで調べてまとめています

# https://www.statsmodels.org/dev/generated/statsmodels.tsa.stattools.adfuller.html
from statsmodels.tsa.stattools import adfuller

# 検定結果を見やすく加工
result = adfuller(flights["passengers"],regression='ct')
labels = ["検定統計量","P値","#ラグ数","#観測数"]
mod_result = pd.Series(result[0:4],index=labels)
for key,val in result[4].items():
    mod_result[f'臨界値 (有意水準:{key})'] = val;
mod_result

検定統計量              -2.100782
P値                  0.545659
#ラグ数               13.000000
#観測数              130.000000
臨界値 (有意水準:1%)      -4.030152
臨界値 (有意水準:5%)      -3.444818
臨界値 (有意水準:10%)     -3.147182
dtype: float64

今回の結果ですと、P値が0.05以下ではないため帰無仮説を棄却できず「単位根がないとは言えない」という結果になります。

つまりUSの国際線乗客数のデータセットは弱定常過程ではなく、非定常過程の可能性がありそうです。

トレンド・季節性・残差の確認 (STL分解)

from statsmodels.tsa.seasonal import STL
res = STL(flights["passengers"]).fit()
res.plot()
plt.show()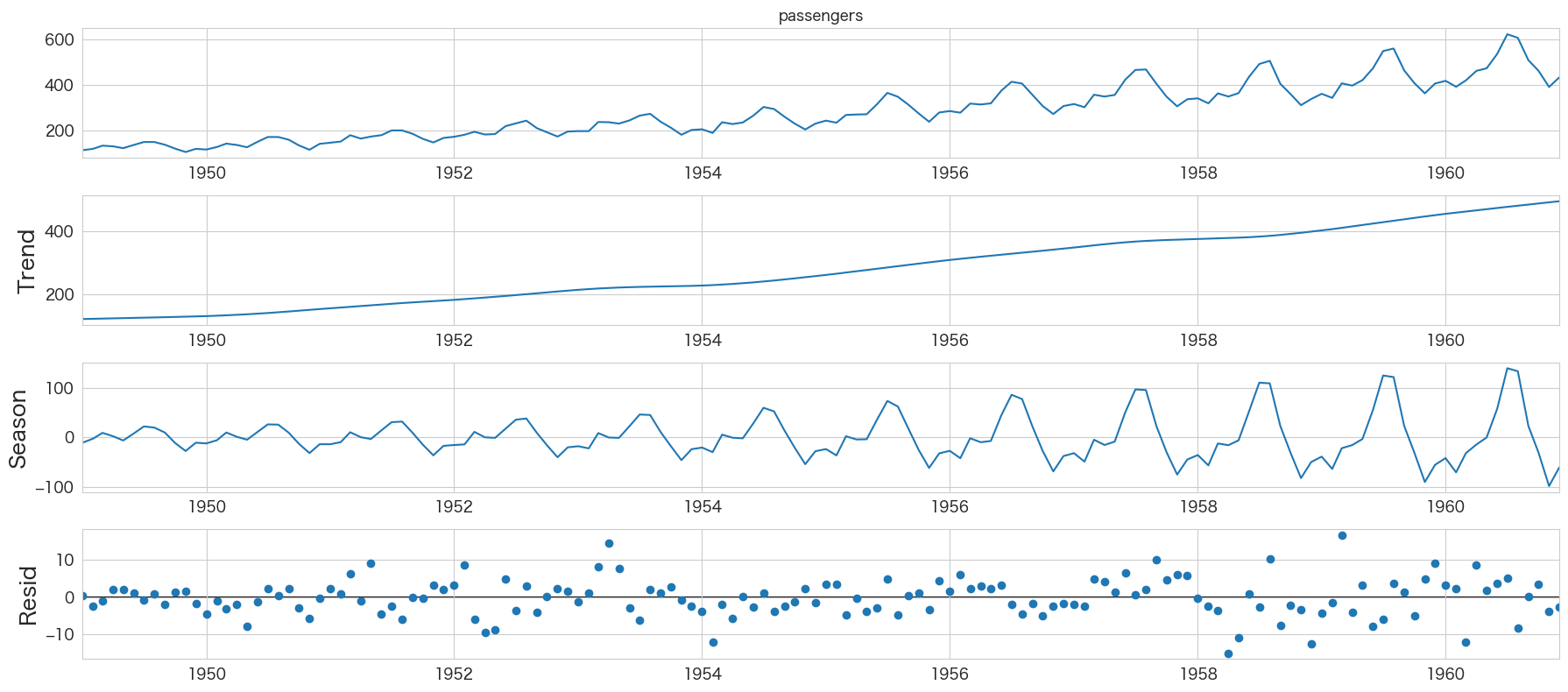

Trendが右肩上がりになっていたり、季節成分が存在することが確認できますね

自己相関係数の確認

時系列分析において現在の値と過去の値の関係を確認します。

python3 -m pip install statsmodels でライブラリをインストールしてください。

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
import numpy as np

fig, ax = plt.subplots(figsize=(16,8))
plot_acf(flights["passengers"], lags=50, zero=False, title="自己相関係数 (autocorrelation)", ax=ax, alpha=0.01)
plt.ylim([0,1])
plt.yticks(np.arange(0.1, 1.1, 0.1))
plt.xticks(np.arange(1, 51, 1))
plt.axhline(y=0.5, color="green")
plt.show()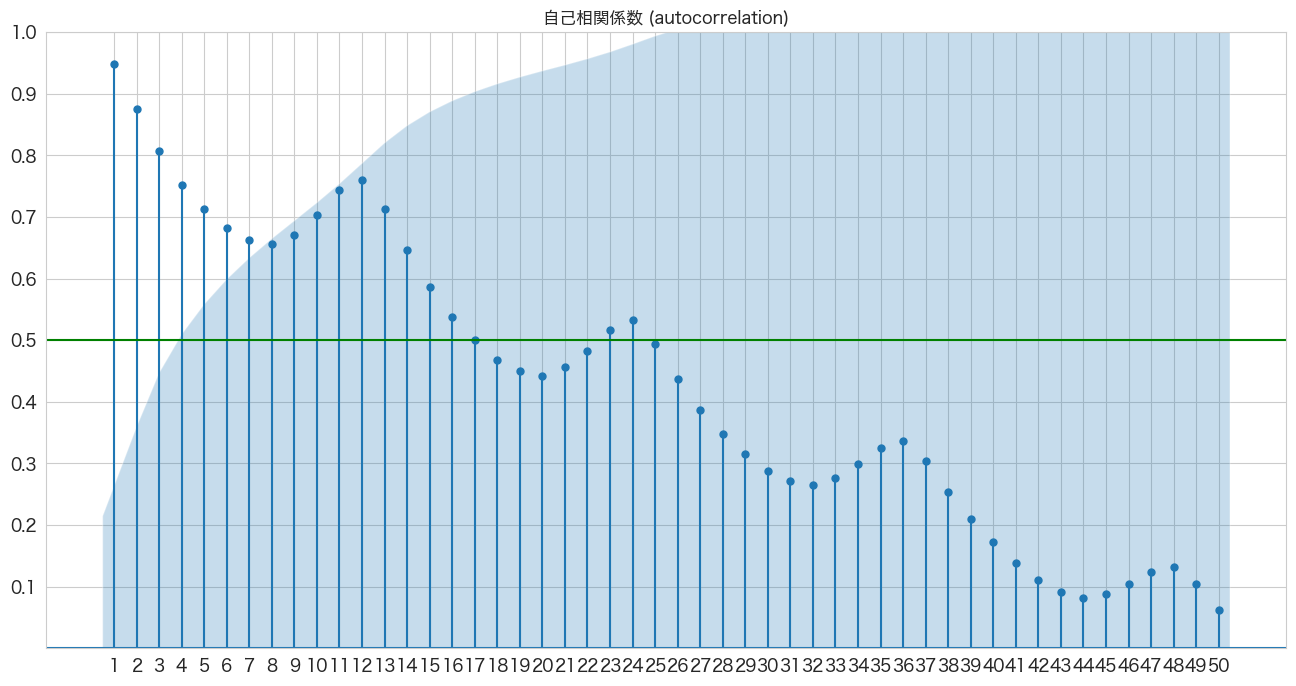

X軸がLag日数で、Y軸が相関係数です。

7ヶ月前くらいまでは関係ありそうですね。

青いエリアは帰無仮説(H0)が「自己相関係数は0である」の信頼区間になっており、青いエリア外にプロットがある場合だと帰無仮説は棄却され「自己相関は0ではない」という結論になるようです。

偏自己相関係数の確認

1つ前のトピックで確認した自己相関係数だと今月の乗客数と3ヶ月前の乗客数の自己相関を確認した場合、2ヶ月前と1ヶ月前の乗客数の影響も含まれています。偏自己相関係数ではこの2ヶ月前と1ヶ月前が与える影響を除外した上で3ヶ月前の乗客数が今月の乗客数にどれくらい関係しているかを確認できるようです。

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_pacf
import numpy as np

fig, ax = plt.subplots(figsize=(16,8))
plot_pacf(flights["passengers"], lags=50, zero=False, title="偏自己相関係数 (partial autocorrelation)", method=('ywm'), ax=ax, alpha=0.01)
plt.ylim([0,1])
plt.yticks(np.arange(0.1, 1.1, 0.1))
plt.xticks(np.arange(1, 51, 1))
plt.axhline(y=0.5, color="green")
plt.show()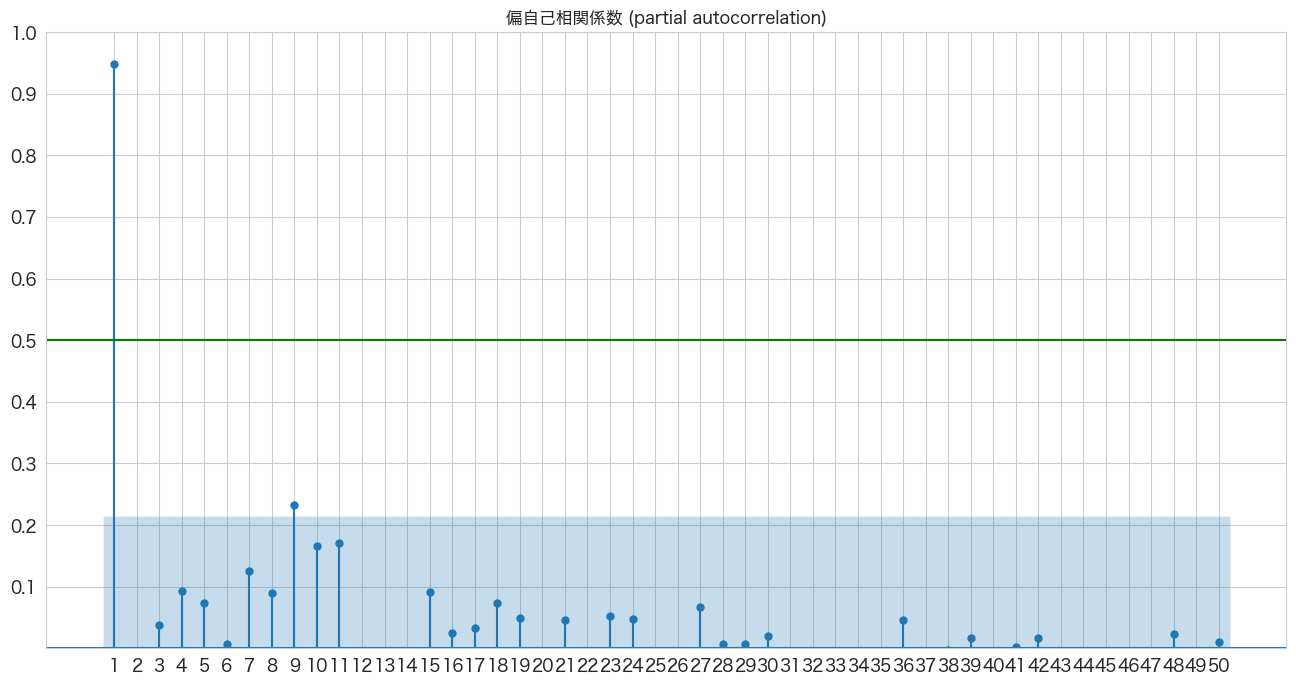

やっぱり今月の乗客数は前月の乗客数が一番関係していそうですね。

(失敗) 非定常過程のデータを定常過程のデータに変換する (1階差)

拡張ディッキー・フラー検定で単位根がないとは言えないという結果になったので、本データセットは非定常過程のデータであると思われます。従ってまずは「階差」によって定常過程のデータに変換できるか確認しようと思います。

# https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.diff.html
# 1階差分を取る
flights_diff1 = flights[["passengers"]].diff(periods=1).dropna()
flights_diff1.head()

  

    

      

      
passengers
    
    

      
ds
      

    
  
  

    

      
1949-02-01
      
6.0
    
    

      
1949-03-01
      
14.0
    
    

      
1949-04-01
      
-3.0
    
    

      
1949-05-01
      
-8.0
    
    

      
1949-06-01
      
14.0
    
  

flights_diff1.passengers.plot()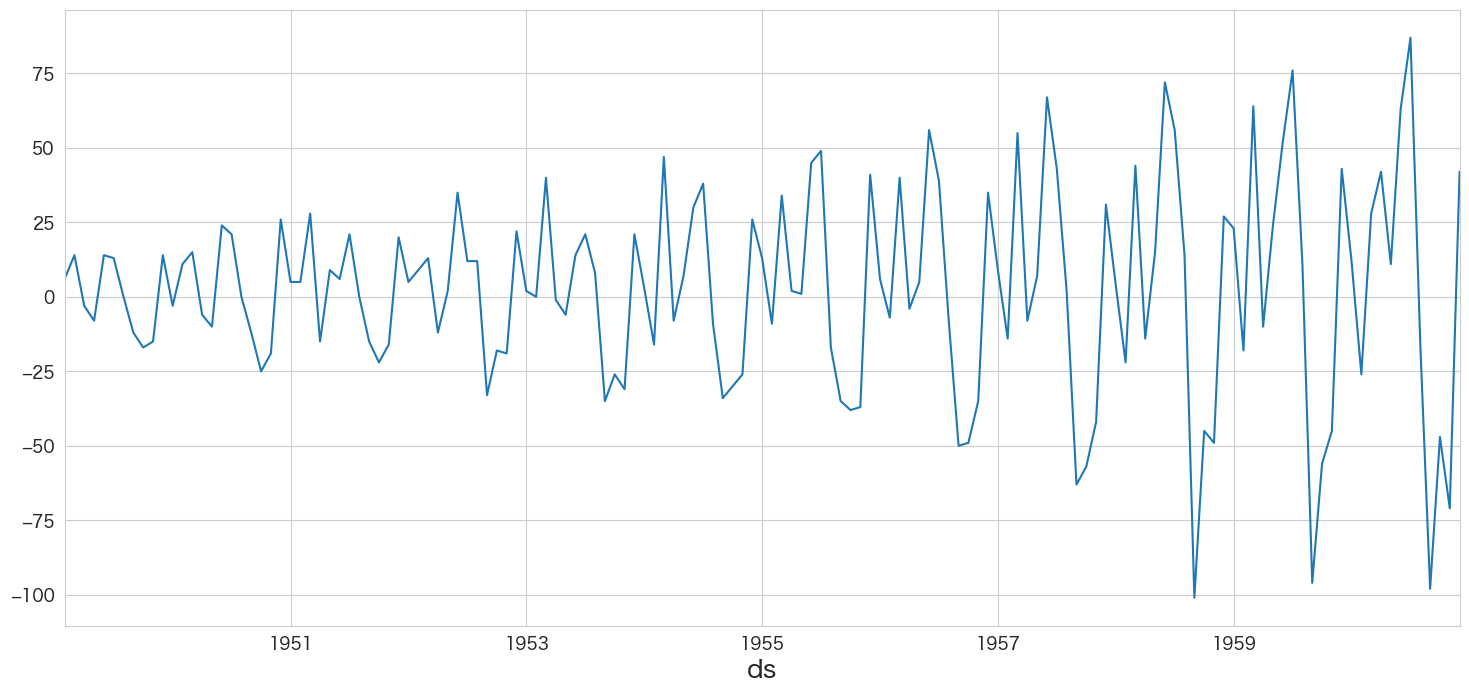

定常過程かどうかと言われると怪しい気がしますね　笑 トレンドの検定とディッキー・フラー検定で確かめてみます。

トレンドの検定

# トレンドの検定
import pymannkendall as mk
mk.original_test(flights_diff1["passengers"])

Mann_Kendall_Test(trend='no trend', h=False, p=0.7178392507093905, z=0.3613480865929473, Tau=0.020486555697823303, s=208.0, var_s=328162.6666666667, slope=0.025974025974025976, intercept=2.1558441558441555)

「トレンドはあるとは言えない」という結果になりました。

定常性の検定

# 定常性の検定
from statsmodels.tsa.stattools import adfuller
# 検定結果を見やすく加工(今回はトレンドがないので、regression='c'に変更した)
result = adfuller(flights_diff1["passengers"],regression='c')
labels = ["検定統計量","P値","#ラグ数","#観測数"]
mod_result = pd.Series(result[0:4],index=labels)
for key,val in result[4].items():
    mod_result[f'臨界値 (有意水準:{key})'] = val;
mod_result

検定統計量              -2.829267
P値                  0.054213
#ラグ数               12.000000
#観測数              130.000000
臨界値 (有意水準:1%)      -3.481682
臨界値 (有意水準:5%)      -2.884042
臨界値 (有意水準:10%)     -2.578770
dtype: float64

1階差分ではP値が0.05以下にはなりませんでした。そのため、帰無仮説を棄却できず「単位根がないとは言えない」という結果になります。つまりまだ非定常なデータの可能性があります。そのため今度は「対数(log)」を取ってみることにします。

(失敗) 非定常過程のデータを定常過程のデータに変換する (対数変換)

乗客数を対数変換してみます。

# https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.diff.html
# 1階差分を取る
flights_log = np.log(flights[["passengers"]])
flights_log.head()

  

    

      

      
passengers
    
    

      
ds
      

    
  
  

    

      
1949-01-01
      
4.718499
    
    

      
1949-02-01
      
4.770685
    
    

      
1949-03-01
      
4.882802
    
    

      
1949-04-01
      
4.859812
    
    

      
1949-05-01
      
4.795791
    
  

# 描画
flights_log.passengers.plot()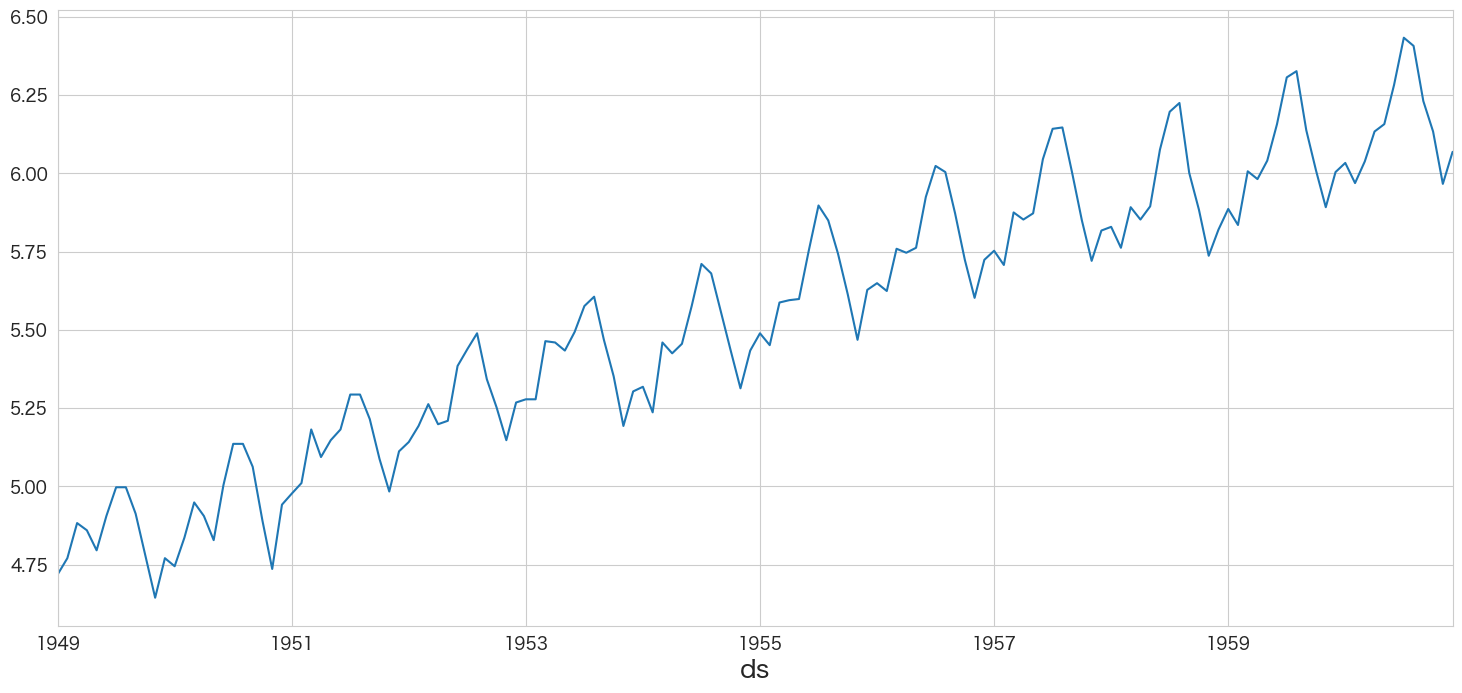

右肩あがりのトレンドはありますが、定常過程になったのでしょうか？トレンドの検定とディッキーフラー検定でまた確認します。

トレンドの検定

# トレンドの検定
import pymannkendall as mk
mk.original_test(flights_log["passengers"])

Mann_Kendall_Test(trend='increasing', h=True, p=0.0, z=14.381610025544802, Tau=0.8087606837606838, s=8327.0, var_s=335164.3333333333, slope=0.00996691105658607, intercept=4.868964740227379)

定常性の検定

# 定常性の検定
from statsmodels.tsa.stattools import adfuller
# 検定結果を見やすく加工(トレンドが存在するので、regression='ct'に変更した)
result = adfuller(flights_log["passengers"],regression='ct')
labels = ["検定統計量","P値","#ラグ数","#観測数"]
mod_result = pd.Series(result[0:4],index=labels)
for key,val in result[4].items():
    mod_result[f'臨界値 (有意水準:{key})'] = val;
mod_result

検定統計量              -2.147030
P値                  0.519681
#ラグ数               13.000000
#観測数              130.000000
臨界値 (有意水準:1%)      -4.030152
臨界値 (有意水準:5%)      -3.444818
臨界値 (有意水準:10%)     -3.147182
dtype: float64

P値 > 0.05なので帰無仮説を棄却出来ませんでした。

(失敗) 非定常過程のデータを定常過程のデータに変換する (対数1階差)

対数に変換した上で1階差とってみます。

# https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.diff.html
# 対数変換し、1階差分を取る
flights_log_diff1 = np.log(flights[["passengers"]]).diff(periods=1).dropna()
flights_log_diff1.head()

  

    

      

      
passengers
    
    

      
ds
      

    
  
  

    

      
1949-02-01
      
0.052186
    
    

      
1949-03-01
      
0.112117
    
    

      
1949-04-01
      
-0.022990
    
    

      
1949-05-01
      
-0.064022
    
    

      
1949-06-01
      
0.109484
    
  

トレンドの検定

# トレンドの検定
import pymannkendall as mk
mk.original_test(flights_log_diff1["passengers"])

Mann_Kendall_Test(trend='no trend', h=False, p=0.7587047356799437, z=-0.307182144350929, Tau=-0.017433270954397714, s=-177.0, var_s=328271.6666666667, slope=-7.021759637614188e-05, intercept=0.019800535127846422)

定常性の検定

何回も使うので、もはや関数化した方が良かったですかね　笑

# 定常性の検定
from statsmodels.tsa.stattools import adfuller
# 検定結果を見やすく加工(トレンドが存在しないので、regression='c'に設定した)
result = adfuller(flights_log_diff1["passengers"],regression='c')
labels = ["検定統計量","P値","#ラグ数","#観測数"]
mod_result = pd.Series(result[0:4],index=labels)
for key,val in result[4].items():
    mod_result[f'臨界値 (有意水準:{key})'] = val;
mod_result

検定統計量              -2.717131
P値                  0.071121
#ラグ数               14.000000
#観測数              128.000000
臨界値 (有意水準:1%)      -3.482501
臨界値 (有意水準:5%)      -2.884398
臨界値 (有意水準:10%)     -2.578960
dtype: float64

むむむ、P値が0.07です。またも帰無仮説を棄却できませんでした。

調べてみると他の方法は「現在の値と移動平均との差分をとる」といった方法があるようですので試してみます。

(失敗) 非定常過程のデータを定常過程のデータに変換する (現在値 - 移動平均値)

# 現在値(t)と移動平均(t)の差分を算出する
flights_ma12 =  flights[["passengers"]].copy()
flights_ma12["passengers_ma"] = flights_ma12[["passengers"]].rolling(window=12).mean()
flights_ma12["passengers_smoothed"] = flights_ma12["passengers"] - flights_ma12["passengers_ma"]

flights_ma12.head(15)

  

    

      

      
passengers
      
passengers_ma
      
passengers_smoothed
    
    

      
ds
      

      

      

    
  
  

    

      
1949-01-01
      
112.0
      
NaN
      
NaN
    
    

      
1949-02-01
      
118.0
      
NaN
      
NaN
    
    

      
1949-03-01
      
132.0
      
NaN
      
NaN
    
    

      
1949-04-01
      
129.0
      
NaN
      
NaN
    
    

      
1949-05-01
      
121.0
      
NaN
      
NaN
    
    

      
1949-06-01
      
135.0
      
NaN
      
NaN
    
    

      
1949-07-01
      
148.0
      
NaN
      
NaN
    
    

      
1949-08-01
      
148.0
      
NaN
      
NaN
    
    

      
1949-09-01
      
136.0
      
NaN
      
NaN
    
    

      
1949-10-01
      
119.0
      
NaN
      
NaN
    
    

      
1949-11-01
      
104.0
      
NaN
      
NaN
    
    

      
1949-12-01
      
118.0
      
126.666667
      
-8.666667
    
    

      
1950-01-01
      
115.0
      
126.916667
      
-11.916667
    
    

      
1950-02-01
      
126.0
      
127.583333
      
-1.583333
    
    

      
1950-03-01
      
141.0
      
128.333333
      
12.666667
    
  

flights_ma12.plot()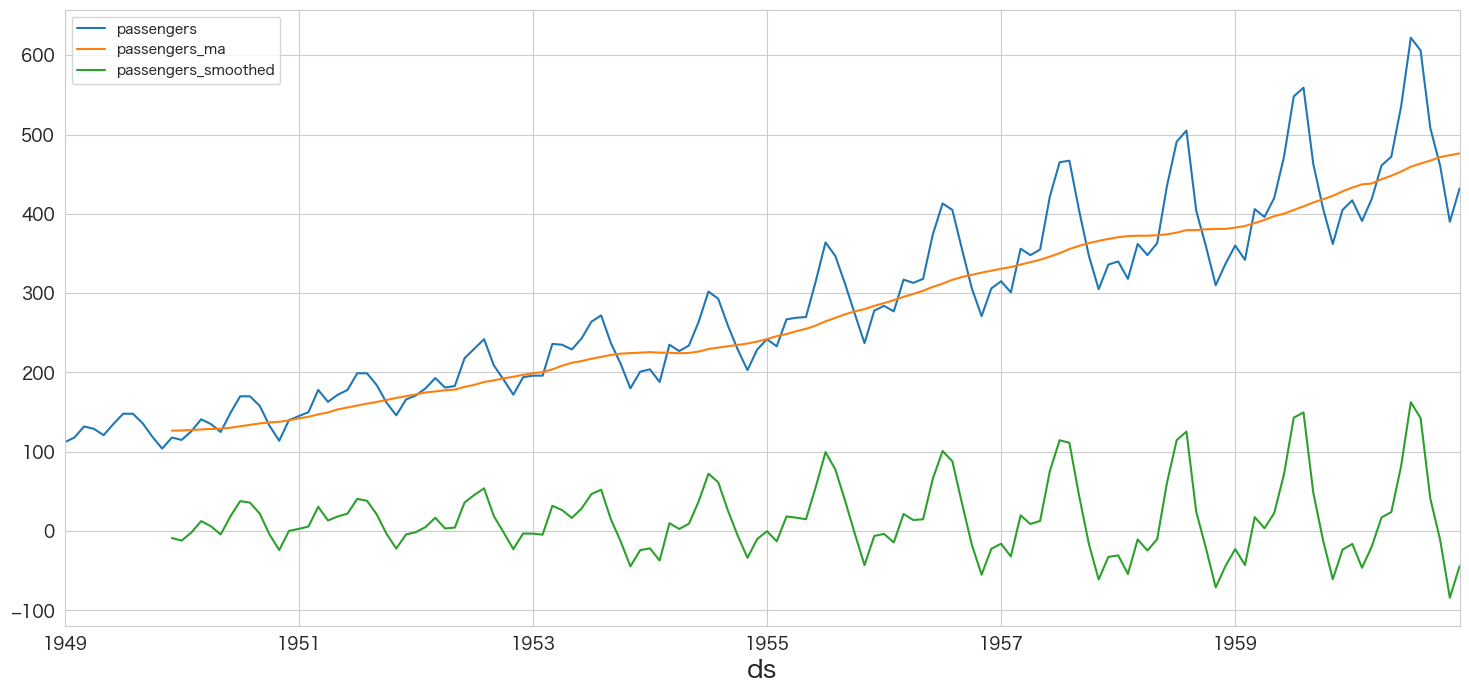

お、緑色の折れ線グラフが定常過程に近づいてきました。後半になるにつれ波が大きくなるので対数変換も追加しようと思います。

Udemyのcomplete-time-series-data-analysis-bootcamp-with-pythonというプログラムで対数変換と移動平均を組み合わせた方法が紹介されていたので、そちらを参考にしました。

(成功) 非定常過程のデータを定常過程のデータに変換する (log(現在値) - 移動平均値)

対数変換した乗客数とその移動平均値を利用してデータの変換してみようと思います。

# データの変換
flights_log_ma12 =  np.log(flights[["passengers"]]).copy()
flights_log_ma12["passengers_ma"] = flights_log_ma12[["passengers"]].rolling(window=12).mean()
flights_log_ma12["passengers_smoothed"] = flights_log_ma12["passengers"] - flights_log_ma12["passengers_ma"]
flights_log_ma12 = flights_log_ma12.dropna()

# 上から5件を確認
flights_log_ma12.head()

  

    

      

      
passengers
      
passengers_ma
      
passengers_smoothed
    
    

      
ds
      

      

      

    
  
  

    

      
1949-12-01
      
4.770685
      
4.836178
      
-0.065494
    
    

      
1950-01-01
      
4.744932
      
4.838381
      
-0.093449
    
    

      
1950-02-01
      
4.836282
      
4.843848
      
-0.007566
    
    

      
1950-03-01
      
4.948760
      
4.849344
      
0.099416
    
    

      
1950-04-01
      
4.905275
      
4.853133
      
0.052142
    
  

flights_log_ma12.plot()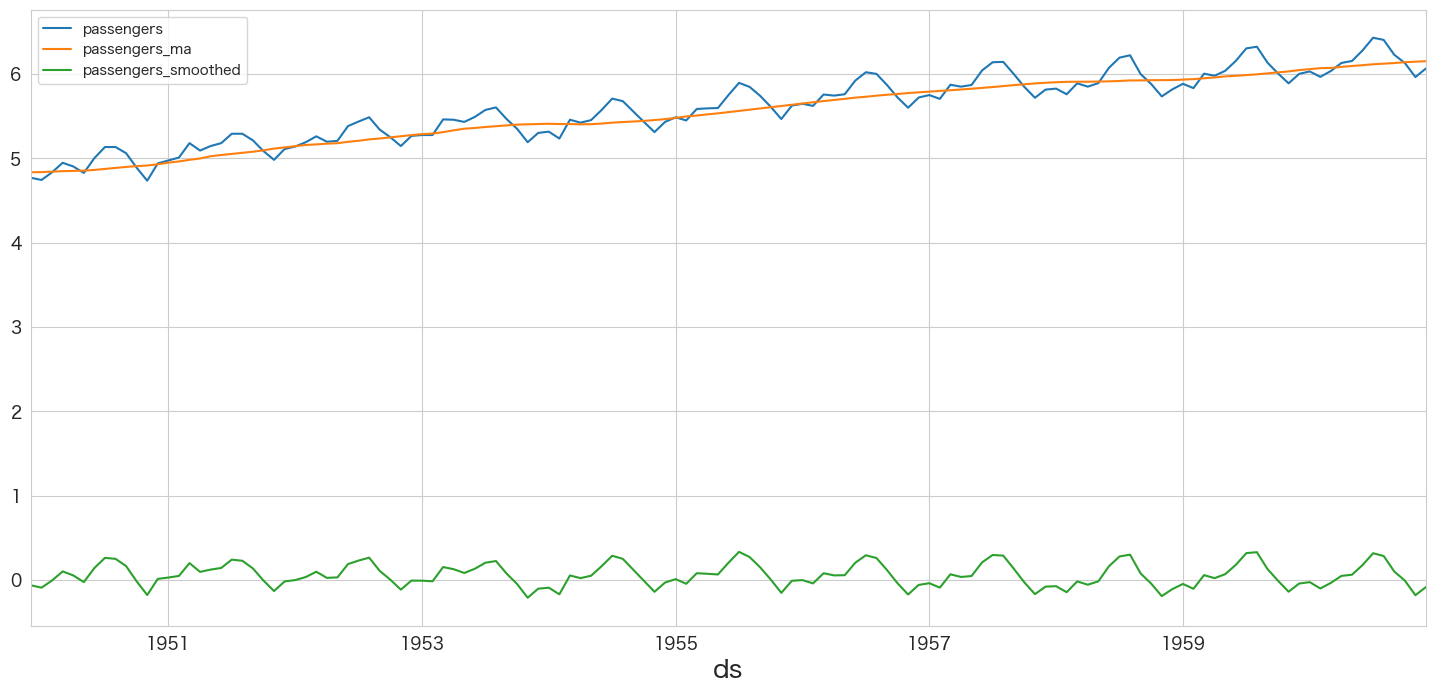

緑の線ですが、いい感じに定常過程っぽくなりました。トレンドと定常性の検定をやってみようと思います。

トレンドの検定

# トレンドの検定
import pymannkendall as mk
mk.original_test(flights_log_ma12["passengers_smoothed"])

Mann_Kendall_Test(trend='no trend', h=False, p=0.34948618250936936, z=-0.9355863941191324, Tau=-0.05491000227842333, s=-482.0, var_s=264315.3333333333, slope=-0.0003134931759312842, intercept=0.06665537246320051)

定常性の検定

# 定常性の検定
from statsmodels.tsa.stattools import adfuller
# 検定結果を見やすく加工(トレンドが存在しないので、regression='c'に設定した)
result = adfuller(flights_log_ma12["passengers_smoothed"],regression='c')
labels = ["検定統計量","P値","#ラグ数","#観測数"]
mod_result = pd.Series(result[0:4],index=labels)
for key,val in result[4].items():
    mod_result[f'臨界値 (有意水準:{key})'] = val;
mod_result

検定統計量              -3.162908
P値                  0.022235
#ラグ数               13.000000
#観測数              119.000000
臨界値 (有意水準:1%)      -3.486535
臨界値 (有意水準:5%)      -2.886151
臨界値 (有意水準:10%)     -2.579896
dtype: float64

やりました。P値 < 0.05なので帰無仮説が棄却され対立仮説である「単位根がない」が採用されます。単位根がないので弱定常過程であるとみなします。

時系列成分の分解

# 時系列成分の分解
from statsmodels.tsa.seasonal import STL
res = STL(flights_log_ma12["passengers_smoothed"]).fit()
res.plot()
plt.show()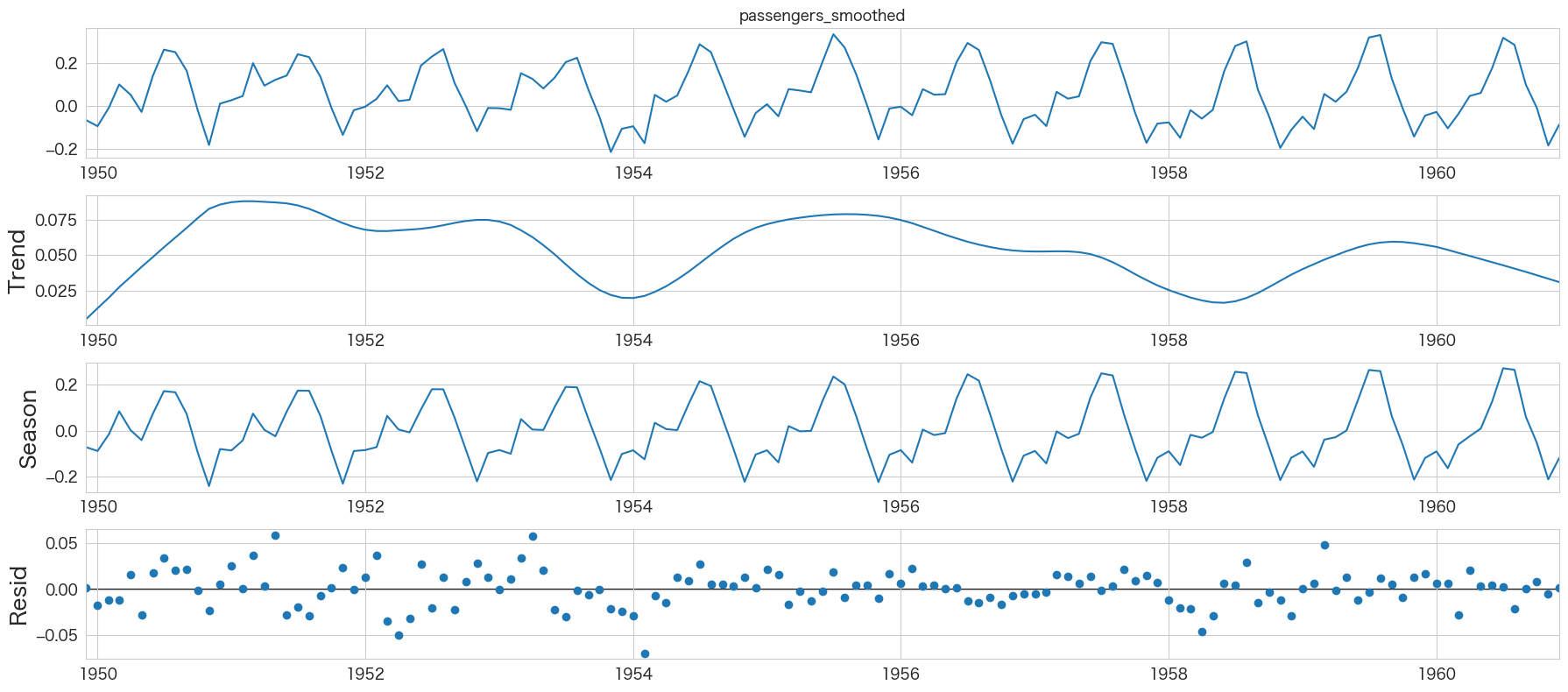

自己相関係数の確認

# 自己相関係数の確認
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
import numpy as np

fig, ax = plt.subplots(figsize=(16,8))
plot_acf(flights_log_ma12["passengers_smoothed"], lags=50, zero=False, title="自己相関係数 (autocorrelation)", ax=ax, alpha=0.01)
plt.ylim([0,1])
plt.yticks(np.arange(0.1, 1.1, 0.1))
plt.xticks(np.arange(1, 51, 1))
plt.axhline(y=0.5, color="green")
plt.show()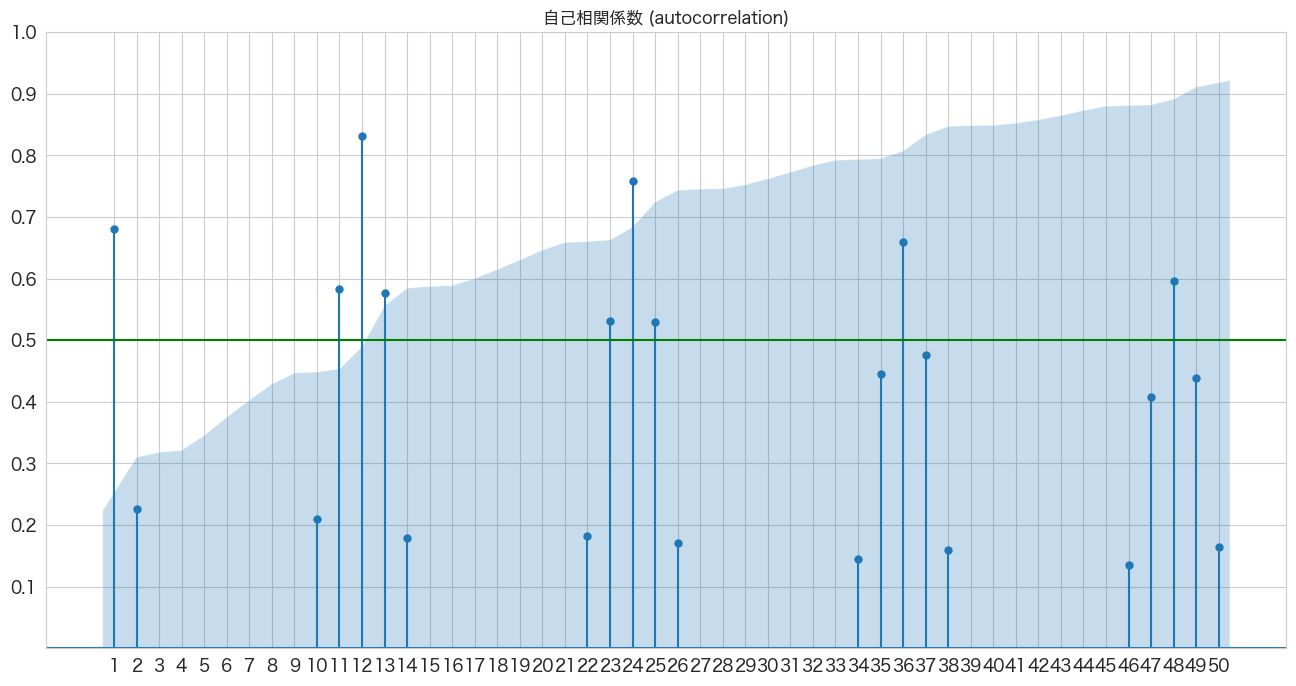

1年ごとの周期性がありそうですね

偏自己相関係数の確認

# 偏自己相関係数の確認
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_pacf
import numpy as np

fig, ax = plt.subplots(figsize=(16,8))
plot_pacf(flights_log_ma12["passengers_smoothed"], lags=50, zero=False, title="偏自己相関係数 (partial autocorrelation)", method=('ywm'), ax=ax, alpha=0.01)
plt.ylim([0,1])
plt.yticks(np.arange(0.1, 1.1, 0.1))
plt.xticks(np.arange(1, 51, 1))
plt.axhline(y=0.5, color="green")
plt.show()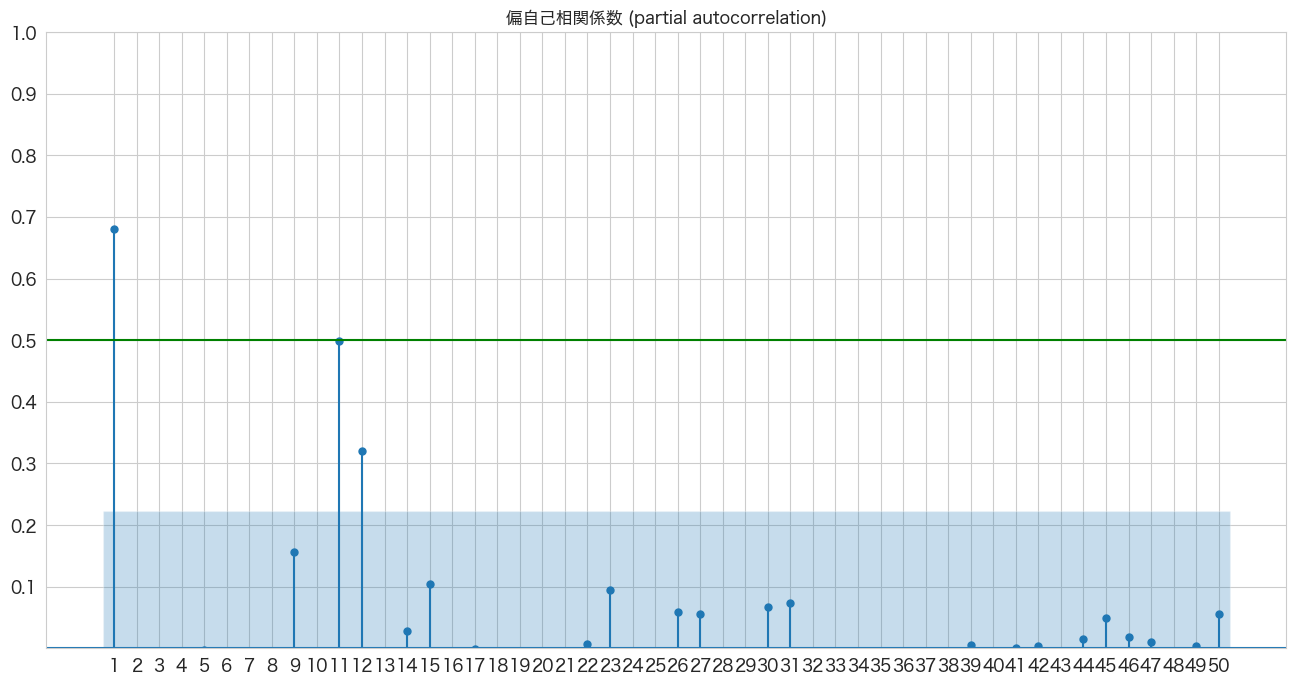

AR(1)、AR(11、AR(12)らへんが青いエリア外(自己相関は0ではない)にあるようです。

ARモデルの作成

まずは、1次のARモデルy_t=C+ϕ₁y_t-1+ε_tを作成します。

訓練データとテストデータに分割

# 訓練用とテスト用に分ける
df = flights_log_ma12.iloc[:-12].copy()  # 1949-12 ~ 1959-12
df_test = flights_log_ma12.iloc[-12:].copy() # 1960-01 ~ 1960-12

1次ARモデルの作成

from statsmodels.tsa.arima.model import ARIMA
ar_model = ARIMA(df["passengers_smoothed"],order=(1,0,0))
ret = ar_model.fit()
ret.summary()

SARIMAX Results

  
Dep. Variable:
   
passengers_smoothed
 
  No. Observations:  
    
121
  


  
Model:
             
ARIMA(1, 0, 0)
    
  Log Likelihood     
  
109.444


  
Date:
             
Sun, 30 Oct 2022
   
  AIC                
 
-212.887


  
Time:
                 
17:03:45
       
  BIC                
 
-204.500


  
Sample:
              
12-01-1949
      
  HQIC               
 
-209.481


  
                    
- 12-01-1959
     
                     
     
 
   


  
Covariance Type:
         
opg
         
                     
     
 
   




     
       
coef
     
std err
      
z
      
P>|z|
  
[0.025
    
0.975]
  


  
const
  
    0.0522
 
    0.027
 
    1.905
 
 0.057
 
   -0.002
 
    0.106


  
ar.L1
  
    0.6788
 
    0.076
 
    8.898
 
 0.000
 
    0.529
 
    0.828


  
sigma2
 
    0.0095
 
    0.002
 
    5.453
 
 0.000
 
    0.006
 
    0.013




  
Ljung-Box (L1) (Q):
     
10.43
 
  Jarque-Bera (JB):  
 
4.76
 


  
Prob(Q):
                
0.00
  
  Prob(JB):          
 
0.09
 


  
Heteroskedasticity (H):
 
1.34
  
  Skew:              
 
-0.05


  
Prob(H) (two-sided):
    
0.36
  
  Kurtosis:          
 
2.03
 



Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

ar.L1のP>|z|が一次ARモデルのϕ係数の有意性になります。0.05以下なので有意で意味のある係数のようです。

2次ARモデルの作成

from statsmodels.tsa.arima.model import ARIMA
# 2次ARモデルの作成
ar_model2 = ARIMA(df["passengers_smoothed"],order=(2,0,0))
ret2 = ar_model2.fit()
ret2.summary()

SARIMAX Results

  
Dep. Variable:
   
passengers_smoothed
 
  No. Observations:  
    
121
  


  
Model:
             
ARIMA(2, 0, 0)
    
  Log Likelihood     
  
121.623


  
Date:
             
Sun, 30 Oct 2022
   
  AIC                
 
-235.245


  
Time:
                 
17:04:17
       
  BIC                
 
-224.062


  
Sample:
              
12-01-1949
      
  HQIC               
 
-230.703


  
                    
- 12-01-1959
     
                     
     
 
   


  
Covariance Type:
         
opg
         
                     
     
 
   




     
       
coef
     
std err
      
z
      
P>|z|
  
[0.025
    
0.975]
  


  
const
  
    0.0564
 
    0.018
 
    3.095
 
 0.002
 
    0.021
 
    0.092


  
ar.L1
  
    0.9677
 
    0.083
 
   11.631
 
 0.000
 
    0.805
 
    1.131


  
ar.L2
  
   -0.4299
 
    0.088
 
   -4.912
 
 0.000
 
   -0.601
 
   -0.258


  
sigma2
 
    0.0078
 
    0.002
 
    4.833
 
 0.000
 
    0.005
 
    0.011




  
Ljung-Box (L1) (Q):
     
0.46
 
  Jarque-Bera (JB):  
 
7.63


  
Prob(Q):
                
0.50
 
  Prob(JB):          
 
0.02


  
Heteroskedasticity (H):
 
1.19
 
  Skew:              
 
0.12


  
Prob(H) (two-sided):
    
0.58
 
  Kurtosis:          
 
1.79



Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

2次ARモデルもar.L1とar.L2はP>|z|が0.05以下なので有意であり意味のある係数のようです。

AR(1)とAR(2)ではどちらが良いモデルなのか、対数尤度比検定(Log likelihood ratio test)で確認をしたいと思います。

対数尤度比検定(Log likelihood ratio test)でAR(1)とAR(2)モデルの結果を比較する

# 参考: https://stackoverflow.com/questions/11725115/p-value-from-chi-sq-test-statistic-in-python
LL1 = ret.llf
LL2 = ret2.llf
LLR = 2 * (LL2-LL1)

from scipy.stats.distributions import chi2
p = chi2.sf(LLR,1).round(3)

if p <= 0.05:
    print(f"p値={p}で有意差あり")
else:
    print(f"p値={p}で有意差なし")

p値=0.0で有意差あり

p値=0.0で有意差あり

有意差ありなのでAR(2)の方が良いモデルという結果になりました。

このように対数尤度比検定を次数を変えたモデルを適用し、最適なARモデルを探索していこうと思います。

最適な次数のARモデルを求める

# Log likelihood ratio testの関数作成
"""
Log likelihood ratio test
H0: 2つのモデルの比に有意差はない
HA: 2つのモデルの比に有意差がある
引数1: モデル1のLog Likelihood
引数2: モデル2のLog Likelihood
引数3: 自由度
リターン: p値
"""
def llr_test(llf1,llf2,dof):
    LL1 = llf1
    LL2 = llf2
    LLR = 2 * (LL2-LL1)

    from scipy.stats.distributions import chi2
    p = chi2.sf(LLR,dof).round(3)

    return p

# warningがでるので非表示にする
import warnings
from statsmodels.tools.sm_exceptions import ConvergenceWarning
warnings.simplefilter('ignore', ConvergenceWarning)
warnings.simplefilter('ignore', UserWarning)

# AR(1) ~ AR(30)までで一番良さそうなモデルを探索する。
from statsmodels.tsa.arima.model import ARIMA
import datetime

best_ar_model_fit = None
alpha=0.05

for i in range(1,31):

    # ARモデル作成
    ar_model = ARIMA(df["passengers_smoothed"],order=(i,0,0))
    ar_model_fit = ar_model.fit()

    # AR(1)は自動的にベストモデルになる
    if i == 1:
        best_ar_model_fit = ar_model_fit
    else:
    # AR(2) 以降の処理
        llf1 = best_ar_model_fit.llf
        llf2 = ar_model_fit.llf
        dof = ar_model_fit.model_orders["ar"] - best_ar_model_fit.model_orders["ar"]
        test_result = llr_test(llf1,llf2,dof)

        if test_result <= alpha:
            # 有意差があれば、ベストモデルを更新
            print(f'llr-test result: compare AR({best_ar_model_fit.model_orders["ar"]}) and AR({ar_model_fit.model_orders["ar"]}) -> p値={test_result}')
            best_ar_model_fit = ar_model_fit
            print(f"{datetime.datetime.now()}: best model is AR({i}) -> Log Likelihood:{best_ar_model_fit.llf}、AIC:{best_ar_model_fit.aic}、BIC:{best_ar_model_fit.bic}、HQIC:{best_ar_model_fit.hqic}")
            print("-----")

llr-test result: compare AR(1) and AR(2) -> p値=0.0
2022-10-30 17:26:31.824075: best model is AR(2) -> Log Likelihood:121.62266525923854、AIC:-235.2453305184771、BIC:-224.0621683360901、HQIC:-230.70342201060802
-----
llr-test result: compare AR(2) and AR(4) -> p値=0.005
2022-10-30 17:26:32.131157: best model is AR(4) -> Log Likelihood:127.01526012353457、AIC:-242.03052024706915、BIC:-225.2557769734887、HQIC:-235.21765748526553
-----
llr-test result: compare AR(4) and AR(6) -> p値=0.0
2022-10-30 17:26:32.846046: best model is AR(6) -> Log Likelihood:135.12400195119895、AIC:-254.2480039023979、BIC:-231.88167953762397、HQIC:-245.16418688665976
-----
llr-test result: compare AR(6) and AR(7) -> p値=0.0
2022-10-30 17:26:33.516660: best model is AR(7) -> Log Likelihood:141.94516938823543、AIC:-265.89033877647086、BIC:-240.72822386610017、HQIC:-255.67104463376543
-----
llr-test result: compare AR(7) and AR(8) -> p値=0.0
2022-10-30 17:26:34.145070: best model is AR(8) -> Log Likelihood:149.7025900506096、AIC:-279.4051801012192、BIC:-251.44727464525175、HQIC:-268.05040883154646
-----
llr-test result: compare AR(8) and AR(9) -> p値=0.018
2022-10-30 17:26:34.944329: best model is AR(9) -> Log Likelihood:152.48701807458718、AIC:-282.97403614917437、BIC:-252.22034014761022、HQIC:-270.4837877525344
-----
llr-test result: compare AR(9) and AR(11) -> p値=0.0
2022-10-30 17:26:37.170329: best model is AR(11) -> Log Likelihood:177.26862464304662、AIC:-328.53724928609324、BIC:-292.1919721933356、HQIC:-313.77604663551875
-----
llr-test result: compare AR(11) and AR(12) -> p値=0.0
2022-10-30 17:26:38.513789: best model is AR(12) -> Log Likelihood:194.08968424664332、AIC:-360.17936849328663、BIC:-321.03830085493223、HQIC:-344.2826887157449
-----
llr-test result: compare AR(12) and AR(13) -> p値=0.0
2022-10-30 17:26:40.032007: best model is AR(13) -> Log Likelihood:215.69509327892735、AIC:-401.3901865578547、BIC:-359.45332837390356、HQIC:-384.3580296533457
-----
llr-test result: compare AR(13) and AR(14) -> p値=0.0
2022-10-30 17:26:41.998918: best model is AR(14) -> Log Likelihood:221.95070135460995、AIC:-411.9014027092199、BIC:-367.16875397967203、HQIC:-393.73376867774357
-----

# ベストモデルのサマリ情報の確認
best_ar_model_fit.summary()

SARIMAX Results

  
Dep. Variable:
   
passengers_smoothed
 
  No. Observations:  
    
121
  


  
Model:
             
ARIMA(14, 0, 0)
   
  Log Likelihood     
  
221.951


  
Date:
             
Sun, 30 Oct 2022
   
  AIC                
 
-411.901


  
Time:
                 
17:34:06
       
  BIC                
 
-367.169


  
Sample:
              
12-01-1949
      
  HQIC               
 
-393.734


  
                    
- 12-01-1959
     
                     
     
 
   


  
Covariance Type:
         
opg
         
                     
     
 
   




     
       
coef
     
std err
      
z
      
P>|z|
  
[0.025
    
0.975]
  


  
const
  
    0.0561
 
    0.007
 
    7.570
 
 0.000
 
    0.042
 
    0.071


  
ar.L1
  
    0.4891
 
    0.079
 
    6.188
 
 0.000
 
    0.334
 
    0.644


  
ar.L2
  
    0.2080
 
    0.096
 
    2.169
 
 0.030
 
    0.020
 
    0.396


  
ar.L3
  
    0.0353
 
    0.069
 
    0.511
 
 0.609
 
   -0.100
 
    0.171


  
ar.L4
  
   -0.1441
 
    0.061
 
   -2.363
 
 0.018
 
   -0.264
 
   -0.025


  
ar.L5
  
    0.0961
 
    0.065
 
    1.481
 
 0.139
 
   -0.031
 
    0.223


  
ar.L6
  
   -0.1449
 
    0.055
 
   -2.625
 
 0.009
 
   -0.253
 
   -0.037


  
ar.L7
  
    0.0202
 
    0.065
 
    0.310
 
 0.756
 
   -0.107
 
    0.148


  
ar.L8
  
   -0.1514
 
    0.065
 
   -2.322
 
 0.020
 
   -0.279
 
   -0.024


  
ar.L9
  
    0.0921
 
    0.073
 
    1.257
 
 0.209
 
   -0.052
 
    0.236


  
ar.L10
 
   -0.1359
 
    0.065
 
   -2.075
 
 0.038
 
   -0.264
 
   -0.008


  
ar.L11
 
    0.0413
 
    0.063
 
    0.652
 
 0.514
 
   -0.083
 
    0.165


  
ar.L12
 
    0.7896
 
    0.066
 
   11.967
 
 0.000
 
    0.660
 
    0.919


  
ar.L13
 
   -0.3509
 
    0.097
 
   -3.616
 
 0.000
 
   -0.541
 
   -0.161


  
ar.L14
 
   -0.3672
 
    0.097
 
   -3.783
 
 0.000
 
   -0.558
 
   -0.177


  
sigma2
 
    0.0012
 
    0.000
 
    7.594
 
 0.000
 
    0.001
 
    0.002




  
Ljung-Box (L1) (Q):
     
1.14
 
  Jarque-Bera (JB):  
 
8.78


  
Prob(Q):
                
0.29
 
  Prob(JB):          
 
0.01


  
Heteroskedasticity (H):
 
0.33
 
  Skew:              
 
0.46


  
Prob(H) (two-sided):
    
0.00
 
  Kurtosis:          
 
3.94



Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

AR(1) ~ AR(30) まで確認をして、AR(14)が良さそうなモデルだという結果になりました。

ar.L14のp値も0.05以下なので有意な係数のようです。

次は作成したモデルが適切かどうか残差分析をしてみます。

作成したARモデルの残差分析

残差の正規性はQQプロットで確認することにします。残差の間に相関がない(独立している)ことはLjung-Box検定で確認します。

resid = best_ar_model_fit.resid
# AR(14)の残差データを確認
resid.plot()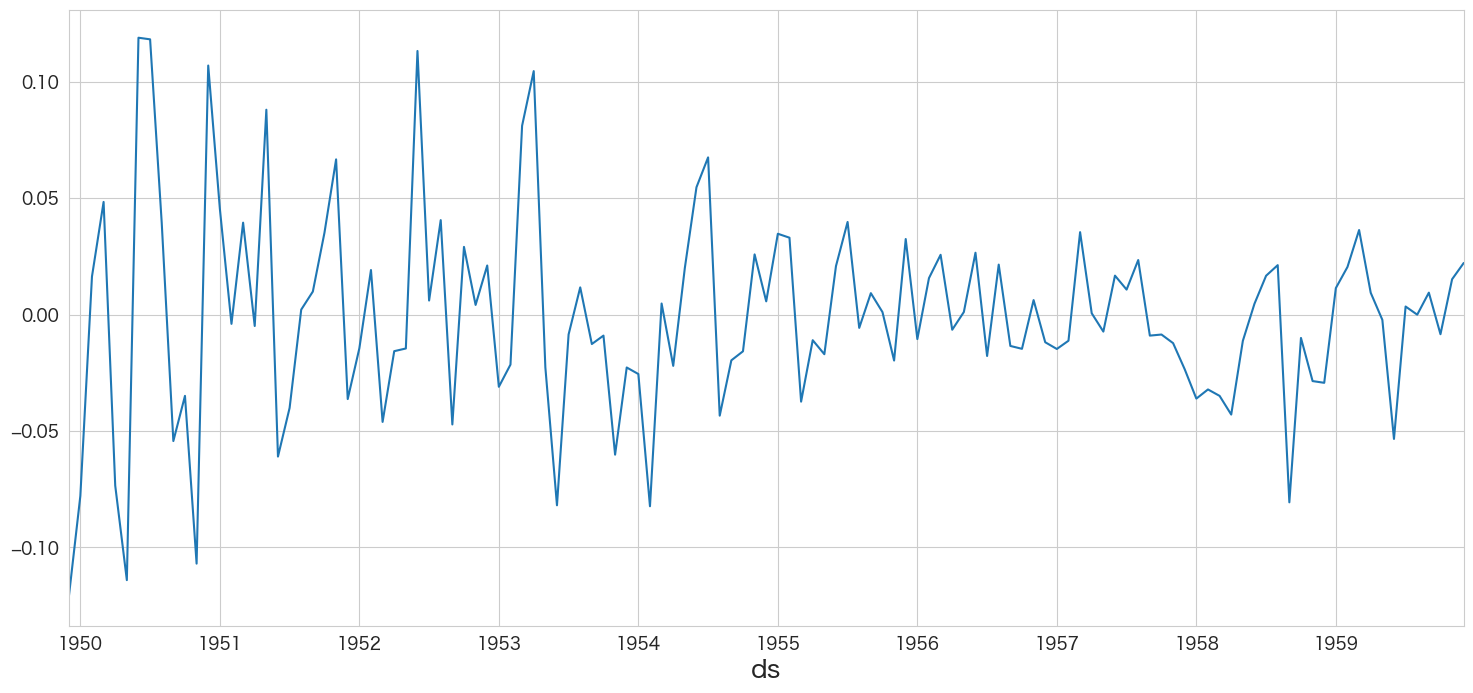

残差の平均と分散を確認

print(f"mean:{resid.mean()}、variance:{resid.var()}")

mean:-0.0008390777653055764、variance:0.001899197988902566

残差の正規性の確認

# 正規分布に従うかどうかをQQプロットを描画して確認
import scipy.stats as stats
import matplotlib.pyplot as plt

plt.subplot(1,2,1)
sns.histplot(resid, kde=True)
plt.subplot(1,2,2)
stats.probplot(resid, dist="norm", plot=plt)
plt.show()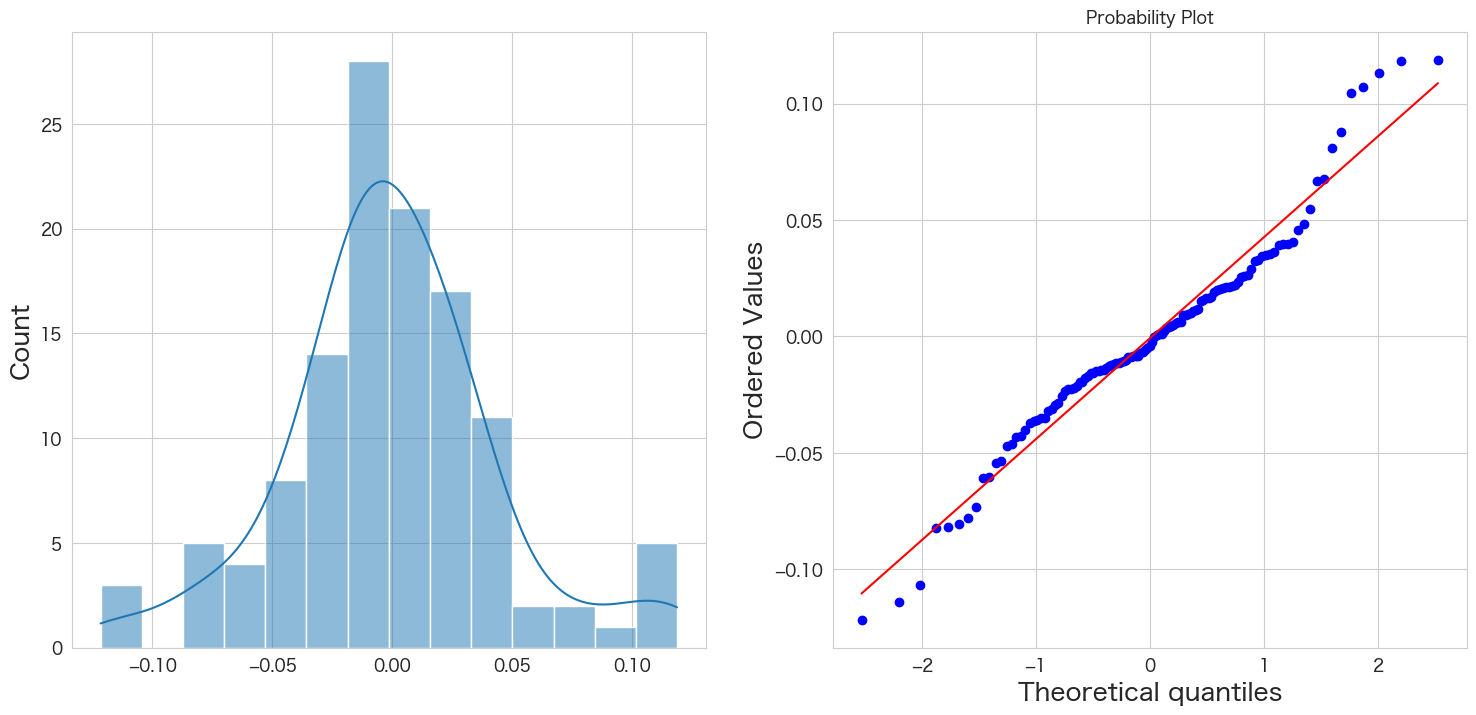

概ね正規分布に従っていそうです。

自己相関係数の確認

# 自己相関係数の確認
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
import numpy as np

fig, ax = plt.subplots(figsize=(16,8))
plot_acf(resid, lags=50, zero=False, title="自己相関係数 (autocorrelation)", ax=ax, alpha=0.01)
plt.ylim([0,1])
plt.yticks(np.arange(0.1, 1.1, 0.1))
plt.xticks(np.arange(1, 51, 1))
plt.show()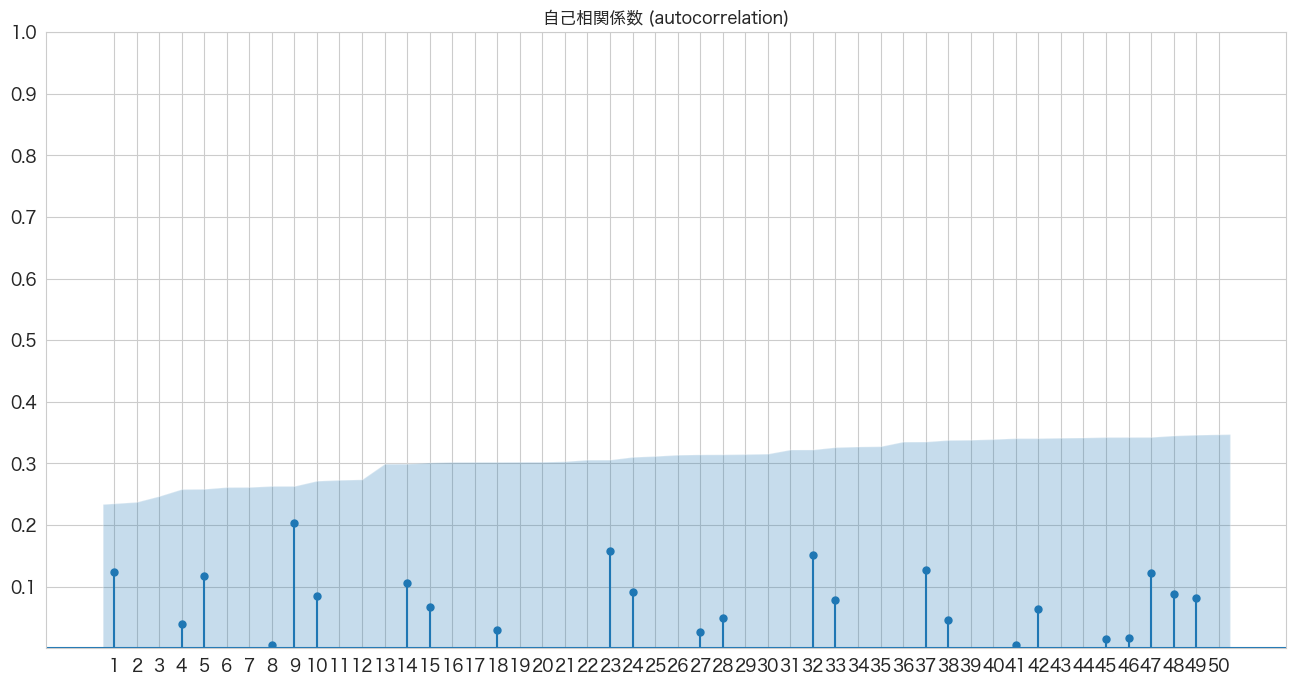

全て青いエリア内なので自己相関はなさそうですね。

Ljung-Box検定で残差の独立性の確認

仮説は下記になります。

H0: 残差は独立分布している
HA: 残差は独立分布ではない

残差が独立分布していることが望ましいので帰無仮説を棄却しない(P値 >= 0.05)結果になることを期待したいと思います。

# https://www.statsmodels.org/stable/generated/statsmodels.stats.diagnostic.acorr_ljungbox.html

import statsmodels.api as sm
#sm.stats.acorr_ljungbox(resid,lags=50)
sm.stats.acorr_ljungbox(resid)

  

    

      

      
lb_stat
      
lb_pvalue
    
  
  

    

      
1
      
1.886589
      
0.169587
    
    

      
2
      
7.139092
      
0.028169
    
    

      
3
      
13.736691
      
0.003286
    
    

      
4
      
13.928157
      
0.007528
    
    

      
5
      
15.695509
      
0.007769
    
    

      
6
      
15.766758
      
0.015062
    
    

      
7
      
16.836716
      
0.018480
    
    

      
8
      
16.840518
      
0.031813
    
    

      
9
      
22.316349
      
0.007929
    
    

      
10
      
23.286251
      
0.009738
    
  

lagが2以上だとp値<=0.05になってしまい「独立分布ではない」という結果になってしまいますね。plot_acfでは自己相関はないとあるのでとりあえずこのまま進めてしまいます。

残差分析の結果

残差分析の結果は、AR(14)の残差が平均0の正規分布に従い、かつ残差の間には相関がない(想定で進める)ので問題ないということにします　笑

AR(14)モデルを使って乗客数を予測する

やっとここまで来ました。作成したARモデルで乗客数を予測したいと思います。

ARモデルの作成

from statsmodels.tsa.arima.model import ARIMA
# 14次ARモデルの作成
ar_model14= ARIMA(flights_log_ma12["passengers_smoothed"],order=(14,0,0))
best_ar_model_fit = ar_model14.fit()

1960-01 ~ 1960-12までの値を予測

best_ar_model_fit.predict(start = df_test.index[0],end = df_test.index[-1]).plot()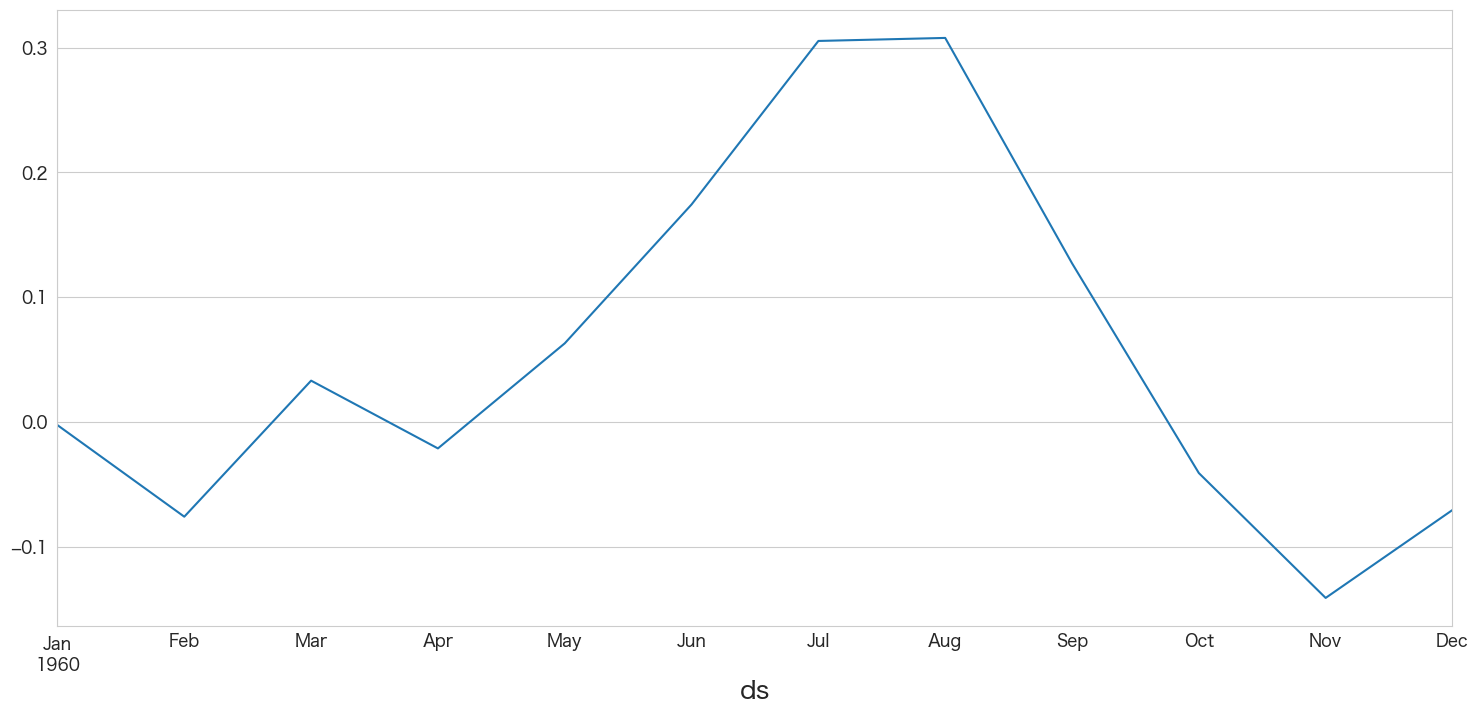

乗客数を定常過程のデータに変換するために12ヶ月の移動平均との差分を取りました。

下記のような式になります。

変換済み乗客数 = log(乗客数) - 12ヶ月の移動平均

「乗客数」の予測をしたいので、対数変換は「log_ab = x と a^^x = b 」のルールに則り元に戻しつつ、移動平均の値も予測して引いてあげる必要があります。

訓練データだとこのような式で元の乗客数の値に戻せます。
np.power(np.e,(df.passengers_smoothed + df.passengers_ma))

移動平均値の予測モデルを作成

t時点の乗客数が分かっていないと移動平均値を出力できないので、単回帰で未来の移動平均値を予測してしまおうと思います。

移動平均線を確認する限り右肩上がりになっているので、単純な線形回帰でも十分予測できると思います。

「線形回帰」は下記でエイムズの住宅価格を予測するときに使っています。

(その4-1) エイムズの住宅価格を単回帰分析で予測してみた

評価指標住宅IdごとのSalePrice(販売価格)を予測するコンペです。評価指標は予測SalePriceと実測SalePriceの対数を取ったRoot-Mean-Squared-Error(RMSE)の値のようです。単回帰分析分析用データ...

www.hinomaruc.com

2022.09.25

# 説明変数と目的変数を指定
X_train = df.index.values.astype(float).reshape(-1, 1) # 月次
# [これでも動いた] X_train = df.index.to_numpy().reshape(-1, 1) 
Y_train = df["passengers_ma"] # 移動平均_乗客数

# 移動平均の予測のため学習
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train,Y_train)

LinearRegression()

# 説明変数の係数を確認
coef = pd.DataFrame()
coef["features"] = ['dt']
coef["coef"] = model.coef_
coef["coef_pct"] = np.abs(coef["coef"]) / np.abs(coef["coef"]).sum()
coef.sort_values(by="coef_pct",ascending=False)

  

    

      

      
features
      
coef
      
coef_pct
    
  
  

    

      
0
      
dt
      
3.947606e-18
      
1.0
    
  

model.intercept_

7.3685329036622385

# 未来の移動平均線の予測
X_test = df_test.index.values.astype(float).reshape(-1, 1)
model.predict(X_test)

array([6.12259268, 6.13316594, 6.14305707, 6.15363033, 6.16386253,
       6.1744358 , 6.18466799, 6.19524126, 6.20581453, 6.21604672,
       6.22661999, 6.23685218])

変換済み乗客数と移動平均の予測

# 予測とデータ変換
df_test["pred_passengers_ma"] = model.predict(X_test)
df_test["pred_passengers_smoothed"] = best_ar_model_fit.predict(start = df_test.index[0],end = df_test.index[-1])
df_test["pred_passengers"] = np.power(np.e,(df_test.pred_passengers_smoothed + df_test.pred_passengers_ma))

plt.figure(figsize=(20, 3))
# 訓練用とテスト用に分ける

ytrue = flights.passengers.iloc[:-12] # 訓練データの実数値
ypred = df_test.pred_passengers # 1960-01 ~ 1960-12の予測値    
ytrue2 = flights.passengers.iloc[-12:] # 1960-01 ~ 1960-12の実測値

plt.plot(ytrue, label="Training Data")
plt.plot(ypred, label="Forecasts")
plt.plot(ytrue2, label="Test Data")

plt.title("airplane passengers prediction")
_ = plt.legend()

青い線が訓練データの実数、緑色の線がテストデータの実数、オレンジの線が予測値になります。

意外にもいい精度で予測できていそうです。(ちょっと上振れて予測されていますかね？)

まとめ

アップル引っ越しは日次データの予測でしたが、今回は国際線乗客数の月次データの予測になります。1年間だけの予測ですがARモデルは非常にマッチしていそうです。

次はいきなりSARIMAモデルを試してみようと思います。

参考

・http://www.hnami.or.tv/d/index.php?%BB%FE%B7%CF%CE%F3%A5%C7%A1%BC%A5%BF%CA%AC%C0%CF

本記事で利用したライブラリのバージョン

import pandas as pd
import numpy as np
import statsmodels as sm
import matplotlib as mpl
import pymannkendall as mk
import scipy as scp
print('pandas',pd.__version__)
print('numpy',np.__version__)
print('statsmodels',sm.__version__)
print('matplotlib',mpl.__version__)
print('pymannkendall',mk.__version__)
print('scipy',scp.__version__)

pandas 1.4.3
numpy 1.23.2
statsmodels 0.13.2
matplotlib 3.5.3
pymannkendall 1.4.2
scipy 1.9.1