前回MAモデルの記事を書きました。

結果はARモデルと同じく1年分の日次予測は難しいかなという結果でした。
今回はARMAモデルを試してみます。
時系列モデル一覧
- AR (自己回帰モデル)
- MA (移動平均モデル)
- ARMA (自己回帰移動平均モデル)
- ARIMA (自己回帰和分移動平均モデル)
- ARIMAX (自己回帰和分移動平均モデル with 外因性変数)
- Auto ARIMA (自動ARIMAモデル)
- SARIMA (季節ARIMAモデル)
- SARIMAX (季節ARIMAモデル with 外因性変数)
- ARCH (分散自己回帰モデル)
- GARCH (一般化分散自己回帰モデル)
- VAR (ベクトル自己回帰モデル)
- VARMA (ベクトル自己回帰移動平均モデル)
※ ARMAモデルについてはWikipedia参照
自己回帰移動平均モデル (…) は自己回帰モデルによる線形フィードバックと移動平均モデルによる線形フィードフォワードによりシステムを表現するモデルである。 (…) ARMAモデルは時系列データの将来値を予測するツールとして機能する。
引用: https://ja.wikipedia.org/wiki/自己回帰移動平均モデル
名前の通りARモデルとMAモデル両方を取り入れたモデルのようです。
- アップル引越しの引越し数をARMAモデルで予想する
- データの読み込み
- 日付の間隔をasfreqメソッドで変更する
- 欠損値の確認
- 引っ越し数(y)を描画
- yが正規分布に従うかどうかQQプロットを確認
- Mann-Kendall trend検定
- 拡張ディッキー・フラー検定で時系列データが(弱)定常か非定常か確認する
- 非定常過程のデータを定常過程のデータに変換する (階差)
- Mann-Kendall trend検定と拡張ディッキー・フラー検定を定常化したデータで確認する
- ARMAモデルの作成
- ARMA(2,2)モデルを作成してARMA(1,1)の結果と比較する
- 最適な次数のMAモデルを求める
- 作成したARMAモデルの残差分析
- ARMA(35,28)モデルを使って引っ越し数を予測する
- (オプション) 残差の予測ではなく、引っ越し数をそのままARMAモデルに投入してみる
- まとめ
- 本記事で利用したライブラリのバージョン
アップル引越しの引越し数をARMAモデルで予想する
モデル作成するパートまではARモデルと共通になります。
本記事では重複した内容になってしまうので、詳細な説明を省きます。
データの読み込み
# アップル引越しのデータセットを読み込む
import pandas as pd
from matplotlib import pyplot as plt
import pandas as pd
# 訓練データと予測付与用データの読み込み
df = pd.read_csv("/Users/hinomaruc/Desktop/blog/dataset/applehikkoshi/train.csv",parse_dates=['datetime'],index_col='datetime')
df_test = pd.read_csv("/Users/hinomaruc/Desktop/blog/dataset/applehikkoshi/test.csv",parse_dates=['datetime'],index_col='datetime')# 描画設定
from IPython.display import HTML
import seaborn as sns
from matplotlib import ticker
import matplotlib.pyplot as plt
sns.set_style("whitegrid")
from matplotlib import rcParams
rcParams['font.family'] = 'Hiragino Sans' # Macの場合
#rcParams['font.family'] = 'Meiryo' # Windowsの場合
#rcParams['font.family'] = 'VL PGothic' # Linuxの場合
rcParams['xtick.labelsize'] = 12 # x軸のラベルのフォントサイズ
rcParams['ytick.labelsize'] = 12 # y軸のラベルのフォントサイズ
rcParams['axes.labelsize'] = 18 # ラベルのフォントとサイズ
rcParams['figure.figsize'] = 18,8 # 画像サイズの変更(inch)日付の間隔をasfreqメソッドで変更する
asfreqメソッドはpandasのメソッドで日付の粒度を変更してくれたり、足りない日付も作成してくれる便利なメソッドです。
# https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.asfreq.html
# 日付の間隔を「日間隔」に変更 (元から日別のデータですが、、週や月間隔にも変更できます)
df = df.asfreq('d')df.info()DatetimeIndex: 2101 entries, 2010-07-01 to 2016-03-31 Freq: D Data columns (total 5 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 y 2101 non-null int64 1 client 2101 non-null int64 2 close 2101 non-null int64 3 price_am 2101 non-null int64 4 price_pm 2101 non-null int64 dtypes: int64(5) memory usage: 98.5 KB
欠損値の確認
df.infoメソッドで確認した通り、欠損値は今回存在しませんのでスキップします。
引っ越し数(y)を描画
pandasのplotメソッドで描画できます。
df.y.plot()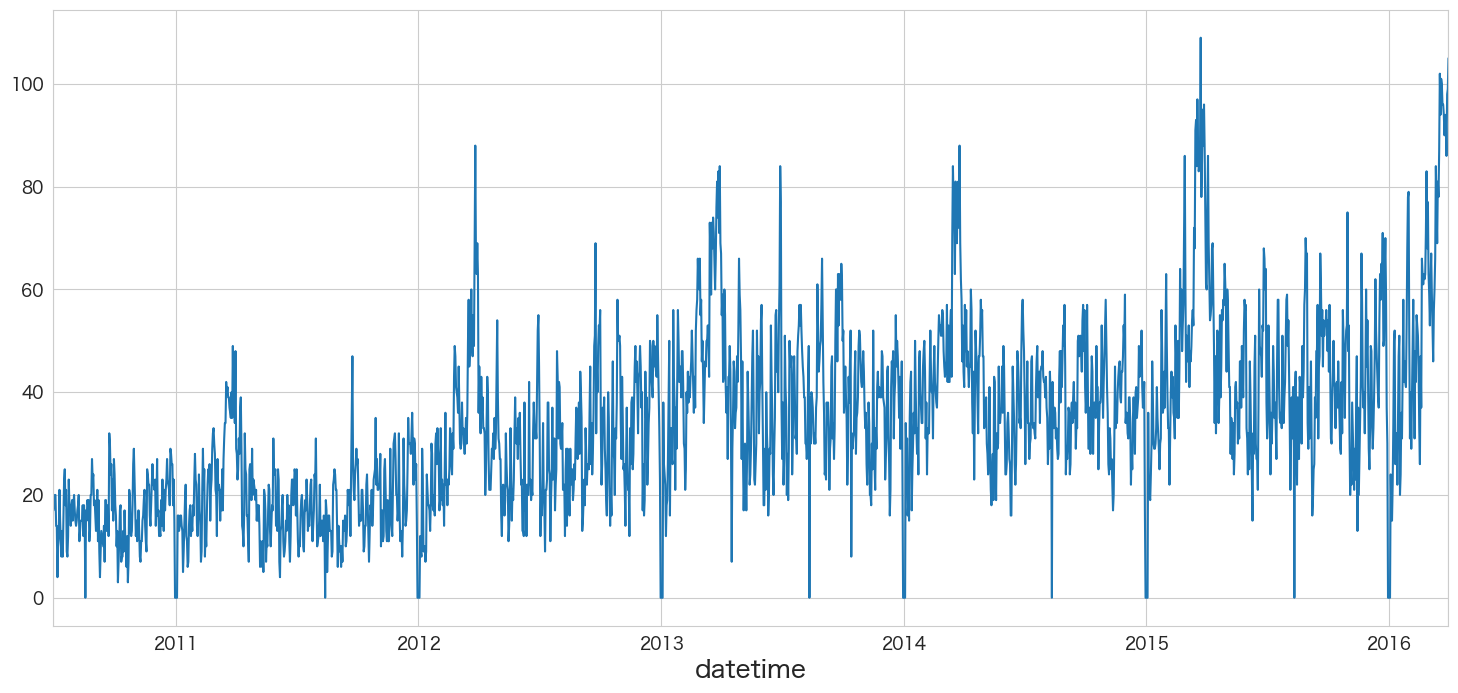
yが正規分布に従うかどうかQQプロットを確認
統計手法を適用するにあたり、おおよそ正規分布を仮定する必要があります。
そのためデータが正規分布に従っているかどうかQQプロットという手法を使って確認します。
# 正規分布に従うかどうかをQQプロットを描画して確認
import scipy.stats as stats
import matplotlib.pyplot as plt
plt.subplot(1,2,1)
sns.histplot(df["y"], kde=True)
plt.subplot(1,2,2)
stats.probplot(df["y"], dist="norm", plot=plt)
plt.show()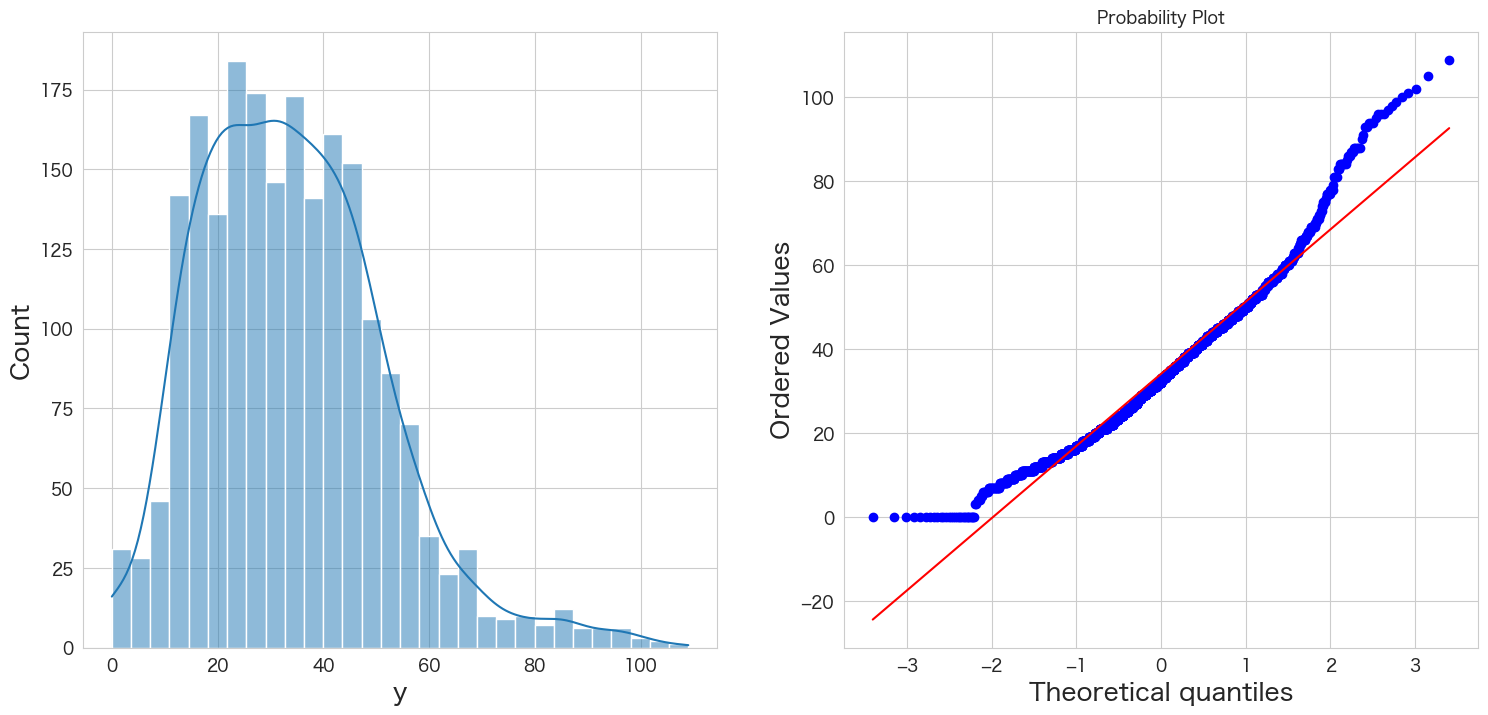
左側のグラフがヒストグラム、右側のグラフがQQプロットです。
青い点が赤い線に沿っていれば正規分布であるという表現方法になっています。
端の部分がずれているようですが、なんとなく正規分布に従っていると仮定します。
Mann-Kendall trend検定
H0: データにトレンドは存在しない
HA: データにトレンドが存在する
# https://pypi.org/project/pymannkendall/
import pymannkendall as mk
mk.original_test(df["y"])Mann_Kendall_Test(trend='increasing', h=True, p=0.0, z=30.51302505819748, Tau=0.4440819564379774, s=979667.0, var_s=1030826418.3333334, slope=0.016624040920716114, intercept=14.544757033248079)
p <= 0.05なので帰無仮説は棄却され、データにトレンドは存在するという結果になりました。
そのため、拡張ディッキー・フラー検定ではトレンドがあるということを示すregression='ct'のオプションを追加しようと思います。
拡張ディッキー・フラー検定で時系列データが(弱)定常か非定常か確認する
帰無仮説と対立仮説は下記になります。
H0: 単位根がある
HA: 単位根がない
# https://www.statsmodels.org/dev/generated/statsmodels.tsa.stattools.adfuller.html
from statsmodels.tsa.stattools import adfuller
# 検定結果を見やすく加工
result = adfuller(df["y"],regression='ct')
labels = ["検定統計量","P値","#ラグ数","#観測数"]
mod_result = pd.Series(result[0:4],index=labels)
for key,val in result[4].items():
mod_result[f'臨界値 (有意水準:{key})'] = val;
mod_result検定統計量 -3.139726 P値 0.097095 #ラグ数 26.000000 #観測数 2074.000000 臨界値 (有意水準:1%) -3.963142 臨界値 (有意水準:5%) -3.412609 臨界値 (有意水準:10%) -3.128298 dtype: float64
P値が0.05以下ではないため帰無仮説を棄却できず「単位根がないとは言えない」という結果になります。
つまりアップル引っ越しのデータセットは弱定常過程ではなく、非定常過程の可能性がありそうです。
非定常過程のデータを定常過程のデータに変換する (階差)
拡張ディッキー・フラー検定で単位根がないとは言えないという結果になったので、本データセットは非定常過程のデータであると思われます。従って階差によって定常過程のデータに変換してモデルを作成します。
# https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.diff.html
# 1階差分を取る
df_diff1 = df.diff(periods=1).dropna()
df_diff1.head()
y client close price_am price_pm datetime 2010-07-02 1.0 0.0 0.0 0.0 0.0 2010-07-03 2.0 0.0 0.0 0.0 0.0 2010-07-04 0.0 0.0 0.0 0.0 0.0 2010-07-05 -6.0 0.0 0.0 0.0 0.0 2010-07-06 0.0 0.0 0.0 0.0 0.0
df_diff1.y.plot()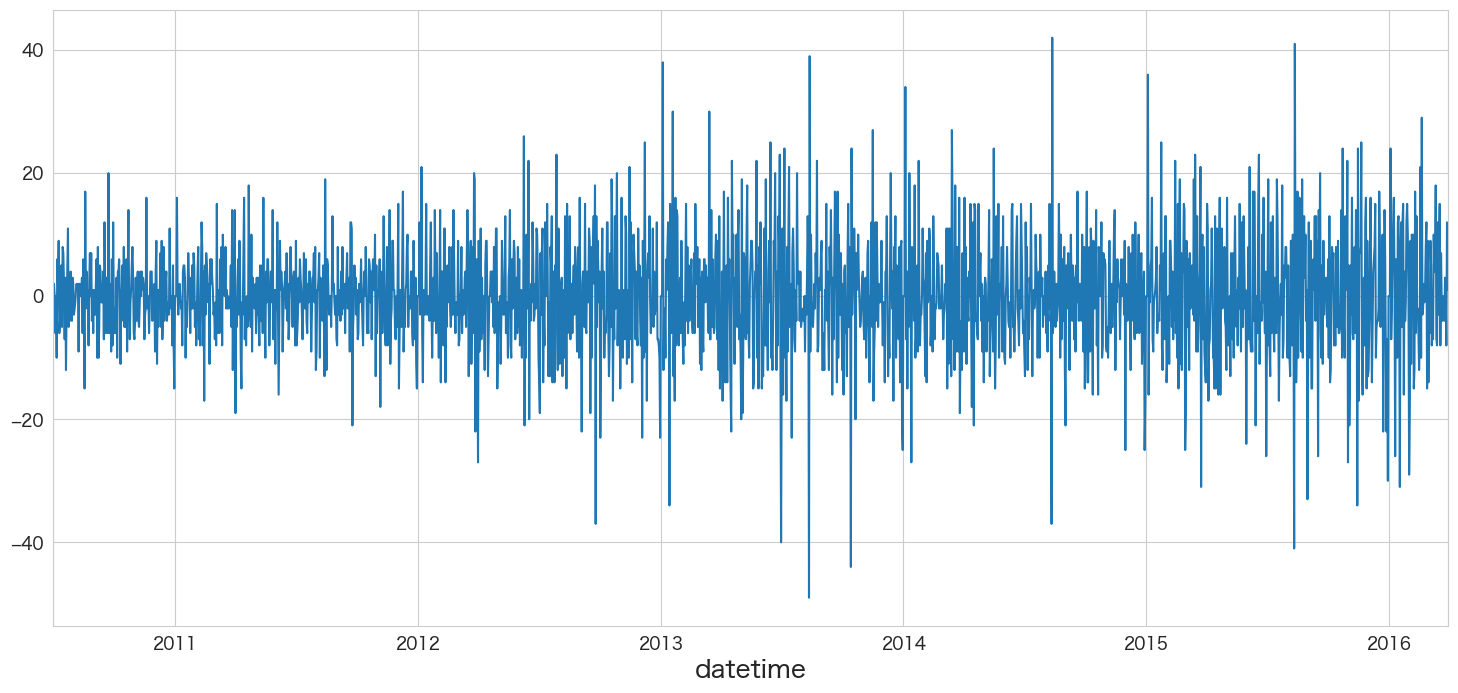
定常過程っぽいデータになりましたね
Mann-Kendall trend検定と拡張ディッキー・フラー検定を定常化したデータで確認する
下記記事と同じ内容になりますので、興味ある方はご確認ください。

まとめると、
・トレンドはなさそう
・(弱)定常過程でありそう
という結果になります。
自己相関係数(ACF)と偏自己相関係数(PACF)の確認
ACFはMAのラグ数、PACFはARのラグ数の指針になるようです。
どちらも自己相関があると思われるラグの値を初期設定としてARMAモデルを構築して調整していくと良いようです。
# 自己相関係数の確認
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf
import numpy as np
fig, ax = plt.subplots(figsize=(16,8))
plot_acf(df_diff1['y'], lags=50, zero=False, title="自己相関係数 (autocorrelation)", ax=ax, alpha=0.01)
plt.ylim([0,1])
plt.yticks(np.arange(0.1, 1.1, 0.1))
plt.xticks(np.arange(1, 51, 1))
plt.axhline(y=0.5, color="green")
plt.show()
fig2, ax2 = plt.subplots(figsize=(16,8))
plot_pacf(df_diff1['y'], lags=50, zero=False, title="偏自己相関係数 (partial autocorrelation)", method=('ywm'), ax=ax2, alpha=0.01)
plt.ylim([0,1])
plt.yticks(np.arange(0.1, 1.1, 0.1))
plt.xticks(np.arange(1, 51, 1))
plt.axhline(y=0.5, color="green")
plt.show()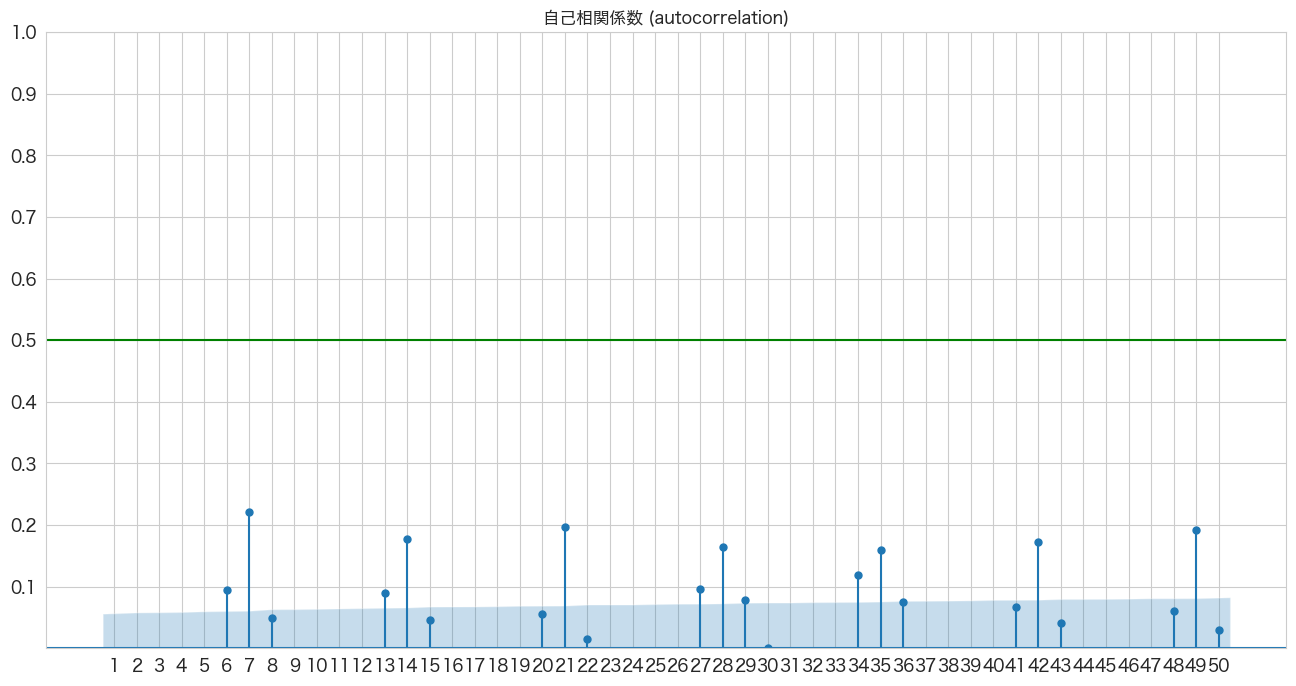
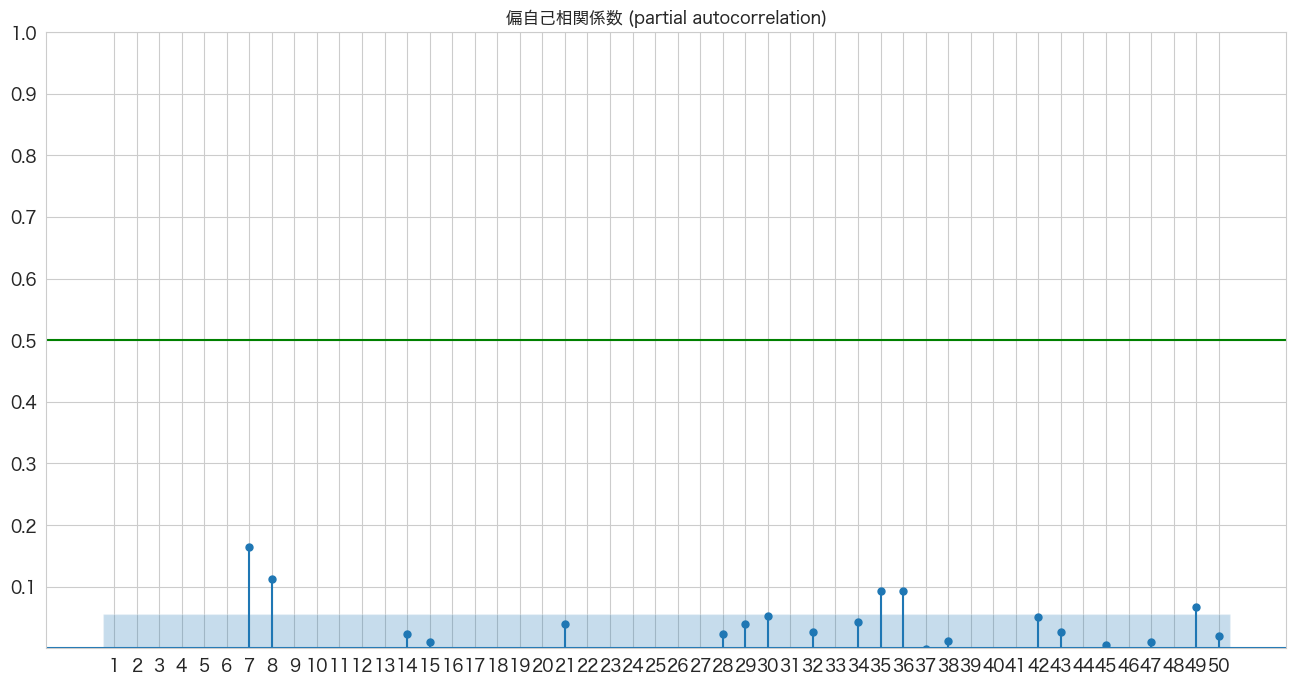
AR=[7,8,35,36]、MA=[7,14,21,28,35,42,49]の組み合わせを試して一番良いモデルのorderを算出した後、係数のP値を確認して妥当なモデルか確認していくという作業になっていくのかなと思います。
ARMAモデルの作成
まずは、ARMA(1,1)のモデルyt=c+ϕ1yt-1 +θ1εt-1+εtを作成していこうと思います。
式の中身を分解すると下記になります。
・cはコンスタント値
・ytは現在の値
・yt-1は1ピリオド前の値
・εtは現在の残差(エラー)
・εt-1は1ピリオド前の残差(エラー)
・ϕは現在値を説明するのに過去の値がどれほど関連しているか (ARの部分)
・θは現在値を説明するのに過去の残差(エラー)がどれほど関連しているか (MAの部分)
ARモデルとMAモデルは対数尤度比検定(Log likelihood ratio test)でモデルん優劣を判断していましたが、簡略化のため、log likelihooodの値とAICの値を判断材料にしようと思います。log likelihooodの値は高いほどいいモデル、AICの値は低いほどいいモデルという判別になります。
それではARMAモデルの作成をしていきたいと思います。
from statsmodels.tsa.arima.model import ARIMA
# ARMA(1,1)モデルの作成
ar1ma1_model = ARIMA(df_diff1.y,order=(1,0,1))
ar1ma1_model_fit = ar1ma1_model.fit()
ar1ma1_model_fit.summary()
SARIMAX Results Dep. Variable: y No. Observations: 2100 Model: ARIMA(1, 0, 1) Log Likelihood -7536.590 Date: Wed, 21 Sep 2022 AIC 15081.180 Time: 16:19:12 BIC 15103.779 Sample: 07-02-2010 HQIC 15089.458 - 03-31-2016 Covariance Type: opg
coef std err z P>|z| [0.025 0.975] const 0.0349 0.038 0.921 0.357 -0.039 0.109 ar.L1 0.6381 0.020 31.392 0.000 0.598 0.678 ma.L1 -0.9284 0.011 -87.638 0.000 -0.949 -0.908 sigma2 76.6691 1.784 42.974 0.000 73.172 80.166
Ljung-Box (L1) (Q): 0.28 Jarque-Bera (JB): 217.27 Prob(Q): 0.60 Prob(JB): 0.00 Heteroskedasticity (H): 2.53 Skew: -0.08 Prob(H) (two-sided): 0.00 Kurtosis: 4.57
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
ar.L1とma.L1のp値は0.0で意味のある係数のようです。AR係数の0.6381プラスの値なので現在と過去の値に正の傾向があるという意味で、MA係数の-0.9284はマイナスの値なので過去の値から離れるという意味のようです。
ARMA(2,2)モデルを作成してARMA(1,1)の結果と比較する
お試しでARMA(2,2)モデルを作成して、ARMA(1,1)とどちらのモデルが良いモデルか比べてみます。
# ARMA(2,2)モデルの作成
ar2ma2_model = ARIMA(df_diff1.y,order=(2,0,2))
ar2ma2_model_fit = ar2ma2_model.fit()
ar2ma2_model_fit.summary()
SARIMAX Results Dep. Variable: y No. Observations: 2100 Model: ARIMA(2, 0, 2) Log Likelihood -7535.822 Date: Wed, 21 Sep 2022 AIC 15083.643 Time: 16:19:22 BIC 15117.541 Sample: 07-02-2010 HQIC 15096.059 - 03-31-2016 Covariance Type: opg
coef std err z P>|z| [0.025 0.975] const 0.0345 0.037 0.936 0.349 -0.038 0.107 ar.L1 0.2290 0.647 0.354 0.723 -1.039 1.497 ar.L2 0.2834 0.408 0.695 0.487 -0.516 1.083 ma.L1 -0.5335 0.650 -0.820 0.412 -1.808 0.741 ma.L2 -0.3729 0.602 -0.619 0.536 -1.554 0.808 sigma2 76.6121 1.781 43.007 0.000 73.121 80.104
Ljung-Box (L1) (Q): 0.02 Jarque-Bera (JB): 219.50 Prob(Q): 0.88 Prob(JB): 0.00 Heteroskedasticity (H): 2.53 Skew: -0.08 Prob(H) (two-sided): 0.00 Kurtosis: 4.58
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
# log likelihoodとAICの値を確認
print(f"ARMA(1,1)\tlog likelihood: {ar1ma1_model_fit.llf}\tAIC: {ar1ma1_model_fit.aic}")
print(f"ARMA(2,2)\tlog likelihood: {ar2ma2_model_fit.llf}\tAIC: {ar2ma2_model_fit.aic}")ARMA(1,1) log likelihood: -7536.590178155023 AIC: 15081.180356310046
ARMA(2,2) log likelihood: -7535.821547414062 AIC: 15083.643094828123log likelihoodの値は ARMA(2.2)の方が高いのですが、AICの値も高くなっているのでARMA(1,1)より良いモデルとは言えないという結果になりました。
確認方法がつかめたのでARMAモデルでARとMAそれぞれの次数の値を探っていこうと思います。
最適な次数のMAモデルを求める
# Log likelihood ratio testの関数作成
"""
Log likelihood ratio test
H0: 2つのモデルの比に有意差はない
HA: 2つのモデルの比に有意差がある
引数1: モデル1のLog Likelihood
引数2: モデル2のLog Likelihood
引数3: 自由度
リターン: p値
"""
def llr_test(llf1,llf2,dof):
LL1 = llf1
LL2 = llf2
LLR = 2 * (LL2-LL1)
from scipy.stats.distributions import chi2
p = chi2.sf(LLR,dof).round(3)
return p# ACFとPACFのグラフを確認した結果のとおり、
# まずはAR=[7,8,35,36]、MA=[7,14,21,28,35,42,49]の組み合わせを試して良さそうなスタートラインを決める
from statsmodels.tsa.arima.model import ARIMA
import datetime
best_arma_model_fit = None
for ar in [7,8,35,36]:
for ma in [7,14,21,28,35,42,49]:
# ARMAモデル作成
arma_model = ARIMA(df_diff1["y"],order=(ar,0,ma))
arma_model_fit = arma_model.fit()
# ARMA(7,7)は自動的にベストモデルになる
if (ar == 7) and (ma==7):
best_arma_model_fit = arma_model_fit
else:
# ARMA(7,7) 以降の処理
llf1 = best_arma_model_fit.llf
aic1 = best_arma_model_fit.aic
llf2 = arma_model_fit.llf
aic2 = arma_model_fit.aic
# llfは高いほど良く、AICは低いほど良い
if llf2 > llf1 and aic2 < aic1:
#条件に合致すれば、ベストモデルを更新
best_arma_model_fit = arma_model_fit
print(f"{datetime.datetime.now()}: best model is ARMA({ar,ma}) -> Log Likelihood:{best_arma_model_fit.llf}、AIC:{best_arma_model_fit.aic}")
print("-----")途中warningが出てしいるのは問題ないようです。
ちなみにConvergenceWarning: Maximum Likelihood optimization failed to convergeはモデルの当てはまりが悪いなどでパラメーターの探索がうまくいってない場合に発生するようです。
This message suggests that the optimizer is having a hard time determining good values for all of the parameters. There are a number of possible reasons why this could happen, but one reason is if the model is not a good fit for your data.
引用: https://github.com/statsmodels/statsmodels/issues/8314
※ warningはアウトプットから削っています。かなり出るのでwarningsをoffにすればよかったかも 2022-09-21 17:08:52.092158: best model is ARMA((7, 14)) -> Log Likelihood:-7326.532247414697、AIC:14699.064494829394 2022-09-21 17:09:37.148874: best model is ARMA((7, 21)) -> Log Likelihood:-7310.3116106352245、AIC:14680.623221270449 2022-09-21 17:11:00.768425: best model is ARMA((7, 28)) -> Log Likelihood:-7302.741788220932、AIC:14679.483576441864 2022-09-21 17:13:16.580240: best model is ARMA((7, 35)) -> Log Likelihood:-7294.690771513018、AIC:14677.381543026037 2022-09-21 17:17:43.116703: best model is ARMA((7, 42)) -> Log Likelihood:-7282.795994795316、AIC:14667.591989590632 2022-09-21 18:06:28.780062: best model is ARMA((35, 14)) -> Log Likelihood:-7272.621157888031、AIC:14647.242315776062 2022-09-21 18:10:09.148433: best model is ARMA((35, 21)) -> Log Likelihood:-7244.432971703251、AIC:14604.865943406501 2022-09-21 18:14:13.904902: best model is ARMA((35, 28)) -> Log Likelihood:-7225.9263071699925、AIC:14581.852614339985
ARMA(35, 28)が選択されました。
# ベストモデルのサマリ情報の確認
best_arma_model_fit.summary()
SARIMAX Results Dep. Variable: y No. Observations: 2100 Model: ARIMA(35, 0, 28) Log Likelihood -7225.926 Date: Wed, 21 Sep 2022 AIC 14581.853 Time: 21:34:58 BIC 14949.083 Sample: 07-02-2010 HQIC 14716.359 - 03-31-2016 Covariance Type: opg
coef std err z P>|z| [0.025 0.975] const 0.0198 0.010 2.034 0.042 0.001 0.039 ar.L1 -0.7257 0.242 -2.999 0.003 -1.200 -0.251 ar.L2 -0.3908 0.184 -2.123 0.034 -0.752 -0.030 ar.L3 0.1043 0.139 0.752 0.452 -0.168 0.376 ar.L4 0.3029 0.131 2.308 0.021 0.046 0.560 ar.L5 0.0886 0.146 0.607 0.544 -0.198 0.375 ar.L6 -0.2113 0.128 -1.653 0.098 -0.462 0.039 ar.L7 -0.3062 0.132 -2.315 0.021 -0.565 -0.047 ar.L8 -0.0558 0.109 -0.514 0.607 -0.268 0.157 ar.L9 0.0316 0.103 0.307 0.759 -0.170 0.233 ar.L10 0.1369 0.103 1.335 0.182 -0.064 0.338 ar.L11 -0.0662 0.088 -0.755 0.450 -0.238 0.106 ar.L12 -0.1526 0.087 -1.746 0.081 -0.324 0.019 ar.L13 -0.2797 0.097 -2.891 0.004 -0.469 -0.090 ar.L14 -0.0338 0.101 -0.335 0.738 -0.232 0.164 ar.L15 0.2545 0.103 2.460 0.014 0.052 0.457 ar.L16 0.0302 0.099 0.306 0.759 -0.163 0.223 ar.L17 -0.0639 0.096 -0.668 0.504 -0.251 0.124 ar.L18 -0.2908 0.087 -3.334 0.001 -0.462 -0.120 ar.L19 -0.2082 0.121 -1.718 0.086 -0.446 0.029 ar.L20 -0.0355 0.108 -0.328 0.743 -0.248 0.177 ar.L21 0.3376 0.102 3.298 0.001 0.137 0.538 ar.L22 0.2314 0.122 1.902 0.057 -0.007 0.470 ar.L23 -0.1042 0.110 -0.943 0.345 -0.321 0.112 ar.L24 -0.5207 0.120 -4.340 0.000 -0.756 -0.286 ar.L25 -0.4876 0.134 -3.641 0.000 -0.750 -0.225 ar.L26 -0.0731 0.125 -0.584 0.559 -0.318 0.172 ar.L27 0.3077 0.108 2.844 0.004 0.096 0.520 ar.L28 0.6300 0.138 4.565 0.000 0.360 0.901 ar.L29 0.1812 0.050 3.656 0.000 0.084 0.278 ar.L30 0.1631 0.040 4.109 0.000 0.085 0.241 ar.L31 0.1870 0.045 4.143 0.000 0.099 0.275 ar.L32 0.2667 0.053 5.038 0.000 0.163 0.370 ar.L33 0.1455 0.054 2.691 0.007 0.039 0.251 ar.L34 0.0781 0.042 1.864 0.062 -0.004 0.160 ar.L35 0.0217 0.036 0.597 0.551 -0.049 0.093 ma.L1 0.2575 0.242 1.065 0.287 -0.217 0.732 ma.L2 -0.0341 0.212 -0.161 0.872 -0.450 0.382 ma.L3 -0.3813 0.187 -2.043 0.041 -0.747 -0.015 ma.L4 -0.4205 0.162 -2.588 0.010 -0.739 -0.102 ma.L5 -0.0920 0.170 -0.543 0.587 -0.424 0.240 ma.L6 0.2480 0.155 1.603 0.109 -0.055 0.551 ma.L7 0.3390 0.155 2.190 0.029 0.036 0.642 ma.L8 -0.0253 0.127 -0.199 0.842 -0.274 0.224 ma.L9 -0.1316 0.124 -1.058 0.290 -0.375 0.112 ma.L10 -0.2298 0.130 -1.774 0.076 -0.484 0.024 ma.L11 0.0072 0.106 0.068 0.946 -0.201 0.215 ma.L12 0.0486 0.108 0.450 0.652 -0.163 0.260 ma.L13 0.2452 0.112 2.194 0.028 0.026 0.464 ma.L14 -0.0268 0.115 -0.233 0.816 -0.252 0.198 ma.L15 -0.3096 0.121 -2.557 0.011 -0.547 -0.072 ma.L16 0.0282 0.113 0.249 0.803 -0.194 0.250 ma.L17 -0.0001 0.113 -0.001 0.999 -0.221 0.221 ma.L18 0.2253 0.108 2.088 0.037 0.014 0.437 ma.L19 0.1103 0.139 0.795 0.427 -0.162 0.382 ma.L20 -0.0456 0.130 -0.352 0.725 -0.300 0.209 ma.L21 -0.3466 0.120 -2.885 0.004 -0.582 -0.111 ma.L22 -0.1843 0.133 -1.389 0.165 -0.444 0.076 ma.L23 0.1885 0.121 1.561 0.119 -0.048 0.425 ma.L24 0.4590 0.137 3.359 0.001 0.191 0.727 ma.L25 0.2895 0.133 2.184 0.029 0.030 0.549 ma.L26 -0.1433 0.125 -1.146 0.252 -0.388 0.102 ma.L27 -0.3896 0.128 -3.041 0.002 -0.641 -0.139 ma.L28 -0.6192 0.155 -3.996 0.000 -0.923 -0.315 sigma2 61.5569 1.735 35.476 0.000 58.156 64.958
Ljung-Box (L1) (Q): 0.01 Jarque-Bera (JB): 324.95 Prob(Q): 0.92 Prob(JB): 0.00 Heteroskedasticity (H): 2.29 Skew: -0.23 Prob(H) (two-sided): 0.00 Kurtosis: 4.87
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
・AR係数のar.L01~ ar.L35のうち18個が P>|z| が 0.05以上で意味をなさない係数
・MA係数のma.L1 ~ ma.L28のうち17個が P>|z| が 0.05以上で意味をなさない係数
でした。
これはもっとシンプルなモデルにできることを示唆しているようですが、今回はこのまま進めていこうと思います。
作成したARMAモデルの残差分析
残差の正規性はQQプロットで確認することにします。残差の間に相関がない(独立している)ことはLjung-Box検定で確認します。
resid = best_arma_model_fit.resid
# ARMA(35,28)の残差データを確認
resid.plot()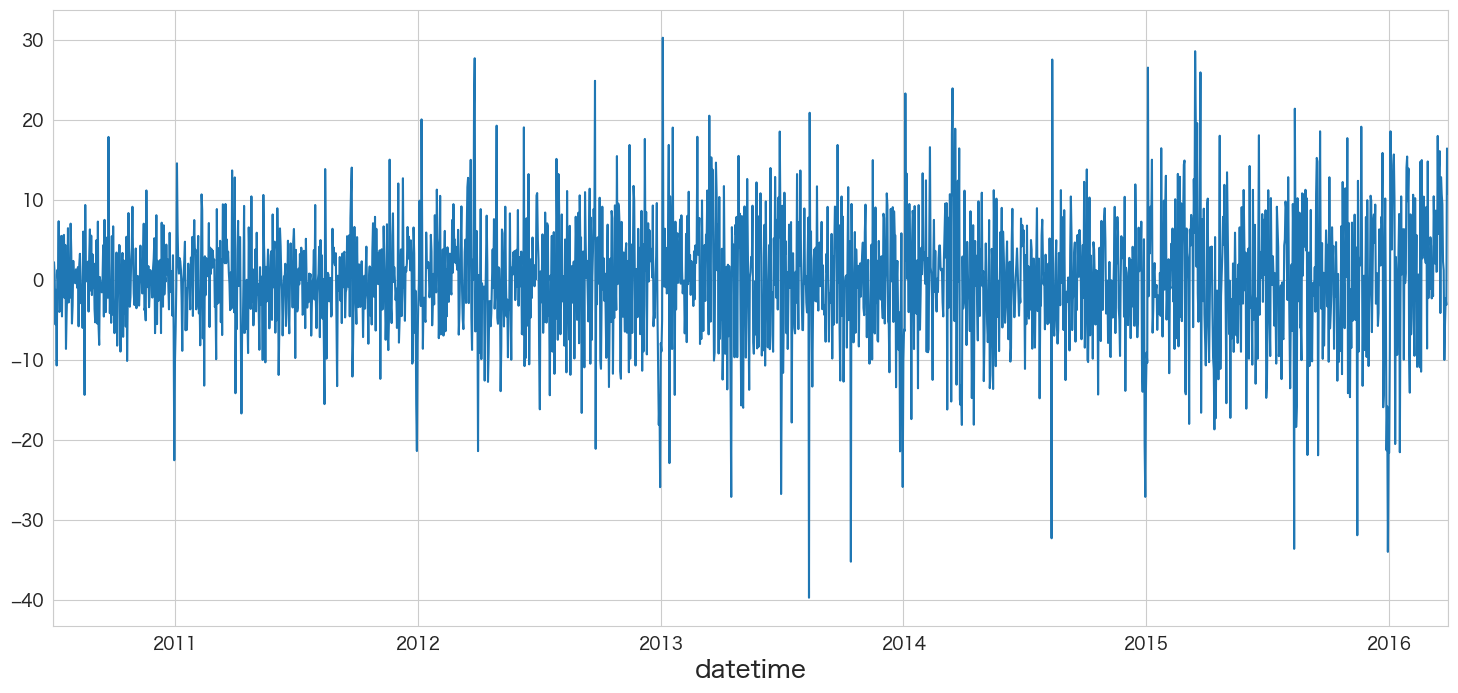
残差の平均と分散を確認
print(f"mean:{resid.mean()}、variance:{resid.var()}")mean:0.0003919578747833204、variance:56.7044965544352
残差の正規性の確認
# 正規分布に従うかどうかをQQプロットを描画して確認
import scipy.stats as stats
import matplotlib.pyplot as plt
plt.subplot(1,2,1)
sns.histplot(resid, kde=True)
plt.subplot(1,2,2)
stats.probplot(resid, dist="norm", plot=plt)
plt.show()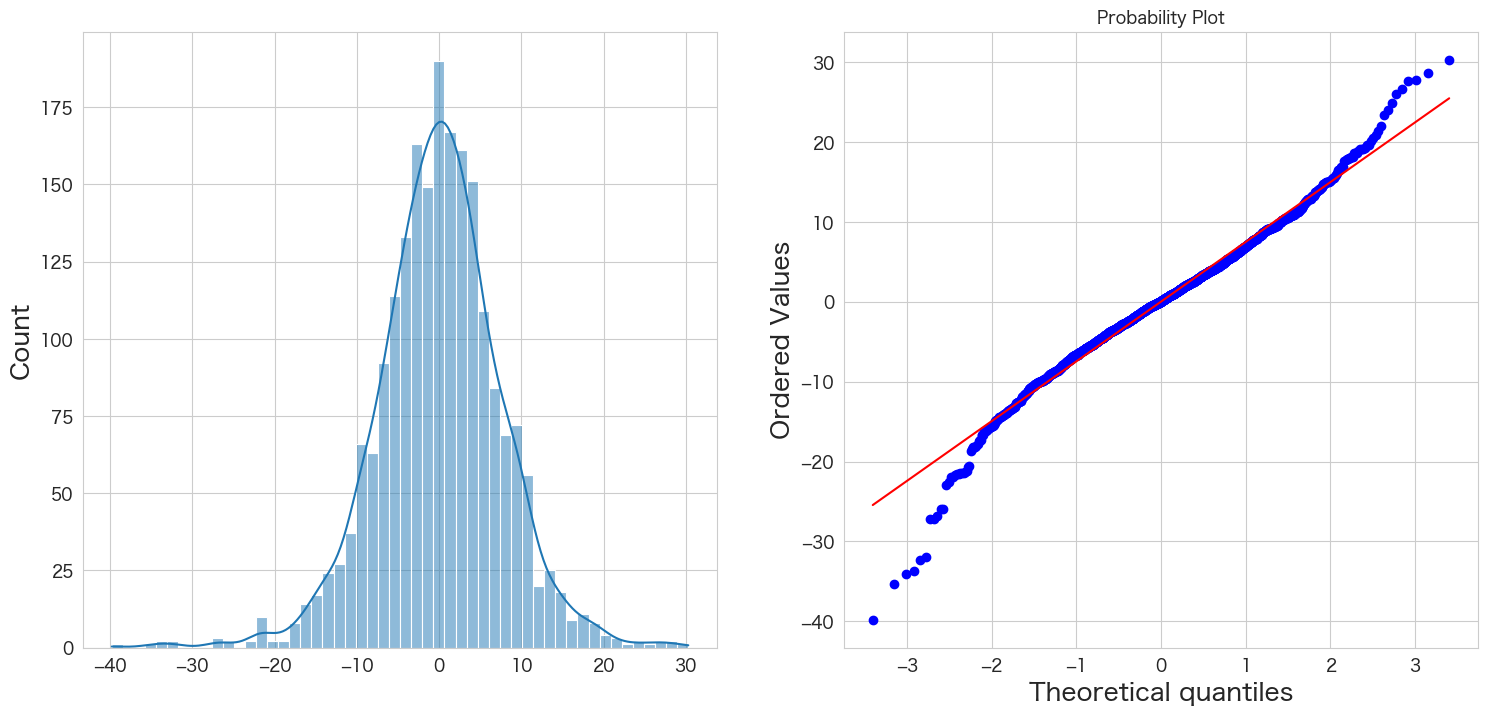
概ね正規分布に従っていそうです。
自己相関係数の確認
# 自己相関係数の確認
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
import numpy as np
fig, ax = plt.subplots(figsize=(16,8))
plot_acf(resid, lags=50, zero=False, title="自己相関係数 (autocorrelation)", ax=ax, alpha=0.01)
plt.ylim([0,1])
plt.yticks(np.arange(0.1, 1.1, 0.1))
plt.xticks(np.arange(1, 51, 1))
plt.show()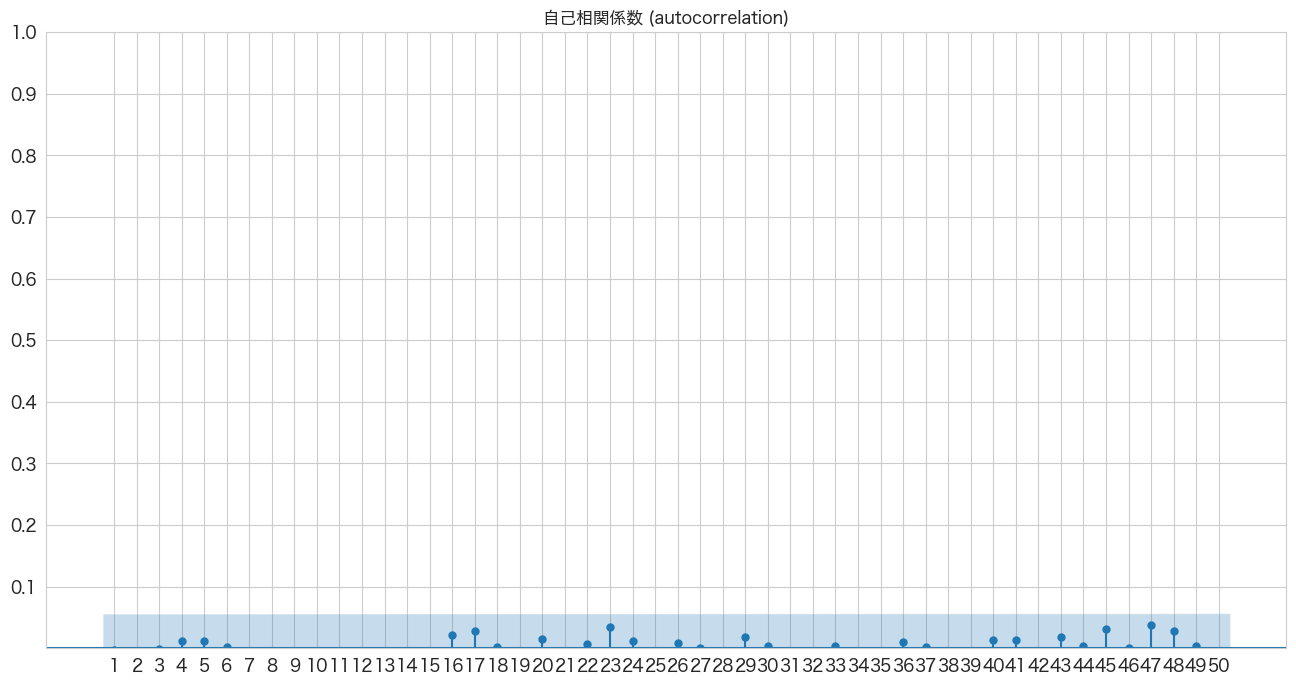
全てのラグが青いエリア内なので問題なさそうです。
Ljung-Box検定で残差の独立性の確認
H0: 残差は独立分布している
HA: 残差は独立分布ではない
残差が独立分布していることが望ましいので帰無仮説を棄却しない(P値 >= 0.05)結果になることを期待したいと思います。
# https://www.statsmodels.org/stable/generated/statsmodels.stats.diagnostic.acorr_ljungbox.html
import statsmodels.api as sm
sm.stats.acorr_ljungbox(resid,lags=50)
lb_stat lb_pvalue 1 0.011686 0.913915 2 0.143040 0.930978 3 0.150921 0.985094 4 0.417733 0.980999 5 0.693918 0.983301 6 0.702819 0.994430 7 1.164911 0.991712 8 2.749300 0.949092 9 3.577558 0.936958 10 5.307432 0.869718 11 5.581831 0.899760 12 6.452172 0.891597 13 7.408150 0.879912 14 8.243099 0.876280 15 8.316958 0.910448 16 9.234596 0.903439 17 10.899463 0.861742 18 10.910356 0.898122 19 10.973101 0.924740 20 11.404043 0.935064 21 11.439417 0.953532 22 11.537977 0.966201 23 14.138049 0.922850 24 14.435594 0.936193 25 14.504890 0.952202 26 14.655830 0.963308 27 14.657846 0.973962 28 15.025384 0.978166 29 15.704724 0.978705 30 15.739981 0.984838 31 16.161825 0.986957 32 16.590876 0.988737 33 16.630544 0.992082 34 16.779439 0.994146 35 18.892458 0.987967 36 19.098703 0.990629 37 19.106045 0.993429 38 19.252047 0.995096 39 19.294917 0.996561 40 19.645050 0.997157 41 20.069758 0.997551 42 20.390804 0.998010 43 21.062967 0.998028 44 21.097238 0.998639 45 23.134654 0.997179 46 23.134671 0.998044 47 26.216152 0.993923 48 27.987032 0.990720 49 28.023933 0.993058 50 28.571382 0.993617
1~50のラグで検定してみました。全てp値が0.05以上なので帰無仮説を棄却できず残差は独立分布ではないとは言えないという結果になりましたので問題なさそうです。
残差分析の結果
残差分析の結果は、ARMA(35,28)の残差が平均0の正規分布に従い、かつ残差の間には相関がありませんでしたので問題ありませんでした。
ARMA(35,28)モデルを使って引っ越し数を予測する
ARモデルとMAモデルの時は長期間の予測は難しそうでしたが、ARMAモデルだとどうなるのでしょうか?楽しみです。
# 2016-04-01 ~ 2017-03-31までの階差を予測
best_arma_model_fit.predict(start = df_test.index[0],end = df_test.index[-1]).plot()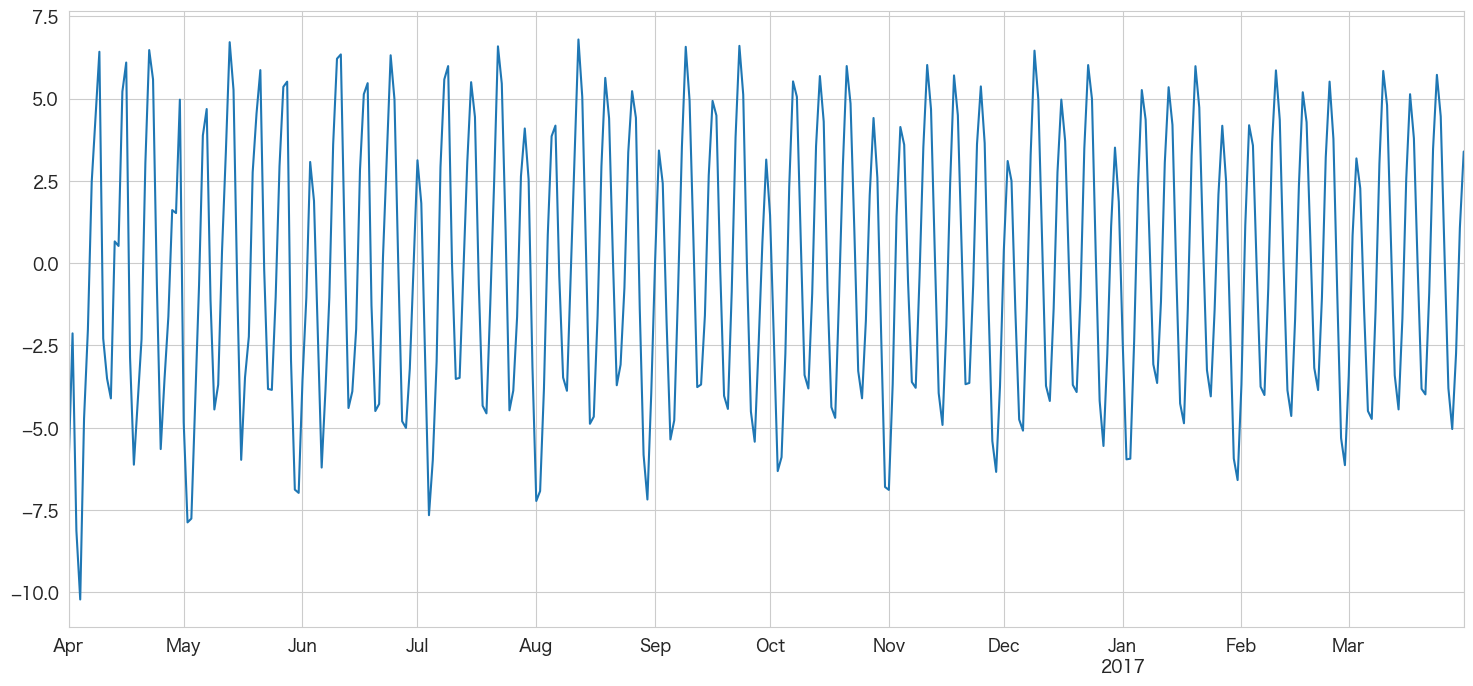
ARモデルのときやMAモデルのときよりは改善されました。
階差の予測値なので引っ越し数の予測値に変換します
# 学習データの一番最後の引っ越し数を確認
df.iloc[-1]y 105 client 1 close 0 price_am 5 price_pm 4 Name: 2016-03-31 00:00:00, dtype: int64
yの値を使います。
predict_diff = best_arma_model_fit.predict(start = df_test.index[0],end = df_test.index[-1])
predict_diff
2016-04-01 -6.041302
2016-04-02 -2.132627
2016-04-03 -8.123813
2016-04-04 -10.215175
2016-04-05 -4.719134
...
2017-03-27 -3.798514
2017-03-28 -5.038416
2017-03-29 -2.744863
2017-03-30 1.081610
2017-03-31 3.390011
Freq: D, Name: predicted_mean, Length: 365, dtype: float64
# 残差予測から引っ越し数の予測値を作成
y_pred = df.y.iloc[-1]
y_pred_list = []
for idx,val in enumerate(predict_diff):
y_pred_list.append((y_pred + val))
# テストデータに予測結果を追加
df_test["y_pred"] = y_pred_list# 学習データの引っ越し数の値(青い線)と予測した引っ越し数の値(オレンジの線)を描画
plt.figure(figsize=(20, 3))
ytrue = df.y.iloc[-31:]
ypred = df_test.y_pred
plt.plot(ytrue, label="Training Data")
plt.plot(ypred, label="Forecasts")
plt.title("apple-hikkoshi prediction")
_ = plt.legend()
39日目以降は横一直線になってしまい予測できていません。またしてもこれでは予測精度を確認しても意味がないので本記事ではここまでの確認とします。
(オプション) 残差の予測ではなく、引っ越し数をそのままARMAモデルに投入してみる
定常データにするために引っ越し数に対して1階差分をとっていましたが、そのまま引っ越し数で予測したらどうなるか試してみます。
とりあえず気にせず同じorderであるARMA(35,28)で作成してみます。
# 引っ越し数を変換かけずに投入し、ARMA(35,28)モデルを作成する
model = ARIMA(df.y,order=(35,0,28))
model_fit = model.fit()
model_fit.summary()
/Users/hinomaruc/Desktop/blog/my-venv/lib/python3.8/site-packages/statsmodels/tsa/statespace/sarimax.py:966: UserWarning: Non-stationary starting autoregressive parameters found. Using zeros as starting parameters.
warn('Non-stationary starting autoregressive parameters'
/Users/hinomaruc/Desktop/blog/my-venv/lib/python3.8/site-packages/statsmodels/tsa/statespace/sarimax.py:978: UserWarning: Non-invertible starting MA parameters found. Using zeros as starting parameters.
warn('Non-invertible starting MA parameters found.'
/Users/hinomaruc/Desktop/blog/my-venv/lib/python3.8/site-packages/statsmodels/base/model.py:604: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
warnings.warn("Maximum Likelihood optimization failed to "
SARIMAX Results
Dep. Variable: y No. Observations: 2101
Model: ARIMA(35, 0, 28) Log Likelihood -7253.589
Date: Thu, 22 Sep 2022 AIC 14637.178
Time: 09:11:05 BIC 15004.439
Sample: 07-01-2010 HQIC 14771.692
- 03-31-2016
Covariance Type: opg
coef std err z P>|z| [0.025 0.975]
const 34.0967 636.834 0.054 0.957 -1214.076 1282.269
ar.L1 -0.6410 1.682 -0.381 0.703 -3.939 2.657
ar.L2 -0.3892 0.816 -0.477 0.633 -1.988 1.209
ar.L3 0.0576 0.804 0.072 0.943 -1.518 1.633
ar.L4 0.2821 0.421 0.671 0.502 -0.542 1.106
ar.L5 0.1041 0.475 0.219 0.826 -0.826 1.034
ar.L6 -0.1403 0.389 -0.361 0.718 -0.902 0.622
ar.L7 -0.3071 0.325 -0.944 0.345 -0.945 0.331
ar.L8 -0.0925 0.622 -0.149 0.882 -1.311 1.126
ar.L9 0.0288 0.219 0.132 0.895 -0.400 0.458
ar.L10 0.2444 0.227 1.079 0.281 -0.200 0.688
ar.L11 0.0341 0.438 0.078 0.938 -0.825 0.893
ar.L12 -0.0736 0.170 -0.433 0.665 -0.406 0.259
ar.L13 -0.1077 0.177 -0.608 0.543 -0.455 0.239
ar.L14 0.1369 0.247 0.554 0.579 -0.347 0.621
ar.L15 0.3513 0.312 1.128 0.259 -0.259 0.962
ar.L16 0.0453 0.577 0.079 0.937 -1.086 1.176
ar.L17 -0.0137 0.181 -0.076 0.940 -0.368 0.340
ar.L18 -0.2680 0.179 -1.496 0.135 -0.619 0.083
ar.L19 -0.1476 0.510 -0.290 0.772 -1.147 0.852
ar.L20 0.1024 0.228 0.449 0.653 -0.344 0.549
ar.L21 0.4672 0.193 2.426 0.015 0.090 0.845
ar.L22 0.2978 0.819 0.364 0.716 -1.307 1.903
ar.L23 -0.0693 0.398 -0.174 0.862 -0.849 0.710
ar.L24 -0.4068 0.241 -1.686 0.092 -0.880 0.066
ar.L25 -0.3653 0.655 -0.558 0.577 -1.649 0.919
ar.L26 -0.0432 0.552 -0.078 0.938 -1.126 1.039
ar.L27 0.1642 0.222 0.739 0.460 -0.271 0.600
ar.L28 0.4254 0.308 1.381 0.167 -0.178 1.029
ar.L29 0.2692 0.759 0.355 0.723 -1.219 1.758
ar.L30 0.2674 0.345 0.774 0.439 -0.409 0.944
ar.L31 0.2097 0.397 0.529 0.597 -0.568 0.987
ar.L32 0.2526 0.291 0.868 0.385 -0.318 0.823
ar.L33 0.1426 0.401 0.356 0.722 -0.643 0.928
ar.L34 0.1248 0.192 0.649 0.517 -0.252 0.502
ar.L35 0.0533 0.207 0.258 0.796 -0.352 0.458
ma.L1 1.1709 1.683 0.696 0.487 -2.128 4.470
ma.L2 1.1645 1.638 0.711 0.477 -2.046 4.375
ma.L3 0.8395 1.867 0.450 0.653 -2.819 4.498
ma.L4 0.4640 1.151 0.403 0.687 -1.792 2.720
ma.L5 0.4160 0.729 0.571 0.568 -1.013 1.845
ma.L6 0.6375 0.543 1.173 0.241 -0.428 1.703
ma.L7 0.9822 0.908 1.082 0.279 -0.797 2.761
ma.L8 0.9301 1.557 0.597 0.550 -2.121 3.982
ma.L9 0.7559 1.349 0.560 0.575 -1.889 3.401
ma.L10 0.4198 1.046 0.401 0.688 -1.631 2.470
ma.L11 0.4221 0.542 0.779 0.436 -0.640 1.484
ma.L12 0.4562 0.647 0.705 0.481 -0.812 1.724
ma.L13 0.5480 0.619 0.885 0.376 -0.666 1.762
ma.L14 0.3911 0.835 0.468 0.640 -1.246 2.028
ma.L15 0.0503 0.542 0.093 0.926 -1.012 1.113
ma.L16 0.1468 0.154 0.953 0.341 -0.155 0.449
ma.L17 0.1667 0.286 0.582 0.560 -0.394 0.728
ma.L18 0.4283 0.277 1.548 0.122 -0.114 0.970
ma.L19 0.4695 0.727 0.646 0.519 -0.956 1.895
ma.L20 0.2890 0.657 0.440 0.660 -0.999 1.577
ma.L21 -0.1022 0.478 -0.214 0.830 -1.038 0.834
ma.L22 -0.2135 0.285 -0.750 0.453 -0.771 0.344
ma.L23 0.0909 0.333 0.273 0.785 -0.562 0.744
ma.L24 0.5241 0.269 1.949 0.051 -0.003 1.051
ma.L25 0.7622 0.831 0.917 0.359 -0.867 2.392
ma.L26 0.6583 1.161 0.567 0.571 -1.617 2.933
ma.L27 0.4631 1.037 0.447 0.655 -1.570 2.496
ma.L28 0.0751 0.723 0.104 0.917 -1.343 1.493
sigma2 61.6912 1.731 35.638 0.000 58.298 65.084
Ljung-Box (L1) (Q): 0.73 Jarque-Bera (JB): 302.75
Prob(Q): 0.39 Prob(JB): 0.00
Heteroskedasticity (H): 2.28 Skew: -0.22
Prob(H) (two-sided): 0.00 Kurtosis: 4.81
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
p値を確認するとほとんど0.05以上なので採用してはいけないモデルかも知れませんが、お試しなのでこのままやります。
# 学習データの引っ越し数の値(青い線)と予測した引っ越し数の値(オレンジの線)を描画
plt.figure(figsize=(20, 3))
ytrue = df.y.iloc[-31:]
ypred = model_fit.predict(start = df_test.index[0],end = df_test.index[-1])
plt.plot(ytrue, label="Training Data")
plt.plot(ypred, label="Forecasts")
plt.title("apple-hikkoshi prediction")
_ = plt.legend()
結果は対して変わらずでした。。
まとめ
ARMAモデルでも1年分の日別予測は難しかったです。
次はAuto ARIMAモデルを試してみたいと思います。
本記事で利用したライブラリのバージョン
import pandas as pd
import numpy as np
import statsmodels as sm
import matplotlib as mpl
import pymannkendall as mk
import scipy as scp
print('pandas',pd.__version__)
print('numpy',np.__version__)
print('statsmodels',sm.__version__)
print('matplotlib',mpl.__version__)
print('pymannkendall',mk.__version__)
print('scipy',scp.__version__)pandas 1.4.3 numpy 1.23.2 statsmodels 0.13.2 matplotlib 3.5.3 pymannkendall 1.4.2 scipy 1.9.1